2013年,国务院常务会议五项加强房地产调控的政策措施,俗称“国五条”.以下是对海口市工薪阶层关于“国五条”态度进行的调查数据,随机抽取了50人,他们月收入的频数分布情况及对“国五条”赞成的人数如下表所示:
| 月收入(单位:百元) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
(Ⅰ)由以上统计数据填写下面2×2列联表并回答是否有99%的把握认为月收入以5500元为分界点对“国五条”的态度有差异;
| 月收入不低于5500元的人数 | 月收入低于5500元的人数 | 合计 |
| 赞成 | a= | c= | |
| 不赞成 | b= | d= | |
| 合计 | | | |
参考公式:k
2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
,其中n=a+b+c+d.
| P(K2≥k) | 0.50 | 0.40 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(Ⅱ)若对月收入在[15,25),[25,35)内的被调查人员中各随机选取两人进行追踪调查,记选中的4人中不赞成“国五条”的人数为ξ,求随机变量ξ的分布列及数学期望.



 一个圆锥的底面半径为2cm,高为6cm,在圆锥内部有一个高为xcm的内接圆柱.(如图为轴截面图)
一个圆锥的底面半径为2cm,高为6cm,在圆锥内部有一个高为xcm的内接圆柱.(如图为轴截面图)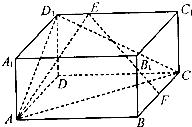 如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=2,AA1=2,F是棱BC的中点,点E在棱C1D1上,且D1E=λEC1(λ为实数).
如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=2,AA1=2,F是棱BC的中点,点E在棱C1D1上,且D1E=λEC1(λ为实数).