
【题目】给出下列说法:
①函数y=2x与函数y=log2x互为反函数;
②若集合A={x|kx2+4x+4=0}中只有一个元素,则k=1;
③若![]() ,则f(x)=x2-2;
,则f(x)=x2-2;
④函数y=log2(1-x)的单调减区间是(-∞,1);
其中所有正确的序号是______.
【答案】①④
【解析】
①利用反函数的定义即可判断出正误;
②若集合A={x|kx2+4x+4=0}中只有一个元素,对k需要分类讨论,k≠0时,利用判别式△=0即可得出;
③没有给出函数f(x)的定义域.
④利用复合函数的单调性即可判断出正误.
①函数y=2x与函数y=log2x互为反函数,正确;
②若集合A={x|kx2+4x+4=0}中只有一个元素,k=0时,方程化为4x+4=0,解得x=﹣1,满足条件;
k≠0时,可得△=16﹣16k=0,解得k=1.综上可得:k=0或1,因此不正确;
③若![]() ,则f(x)=x2﹣2,定义域为{x|x≥0},因此不正确;
,则f(x)=x2﹣2,定义域为{x|x≥0},因此不正确;
④函数y=log2(1﹣x)的单调减区间是(﹣∞,1),正确.
其中所有正确的序号是①④.
故答案为:①④.


科目:高中数学 来源: 题型:
【题目】某厂生产一种机器的固定成本为0.5万元,但每生产100台,需要加可变成本(即另增加投入)0.25万元,市场对此产品的年求量为500台,销售的收入函数为![]() (万元)(
(万元)(![]() ),其中
),其中![]() 是产品售出的数量(单位:百台).
是产品售出的数量(单位:百台).
(1)把利润表示为年产量的函数;
(2)年产量是多少时,工厂所得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() (a>0,b>0)的左焦点为F(-c,0)(c>0),过点F作圆x2+y2=
(a>0,b>0)的左焦点为F(-c,0)(c>0),过点F作圆x2+y2=![]() 的一条切线交圆于点E,交双曲线右支于点P,若
的一条切线交圆于点E,交双曲线右支于点P,若![]() ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A. ![]() B.
B. ![]()
C. ![]() D. 2
D. 2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 的中点,
的中点,![]() 分别是
分别是![]() 的中点,将四边形
的中点,将四边形![]() ,
,![]() 分别沿
分别沿![]() ,
,![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,如图2所示,
,如图2所示,![]() 是
是![]() 上一点,且
上一点,且![]() .
.

(1)求证:![]() ;
;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式ax2-5x+b>0的解是-3<x<2,设A={x|bx2-5x+a>0},B={x|![]() }.
}.
(1)求a,b的值;
(2)求A∩B和A∪(UB).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心
的圆心![]() 在抛物线
在抛物线![]() 上,圆
上,圆![]() 过原点且与抛物线的准线相切.
过原点且与抛物线的准线相切.
(1)求该抛物线的方程;
(2)过抛物线焦点![]() 的直线
的直线![]() 交抛物线于
交抛物线于![]() ,
, ![]() 两点,分别在点
两点,分别在点![]() ,
, ![]() 处作抛物线的两条切线交于
处作抛物线的两条切线交于![]() 点,求三角形
点,求三角形![]() 面积的最小值及此时直线
面积的最小值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】几千年的沧桑沉淀,凝练了西樵山的美,清幽秀丽的自然风光,文化底蕴厚重的旅游,古朴自然的民俗风情.自明清以来,文人雅士,群贤毕至,旅人游子,纷至沓来,使秀美的西樵山成为名嗓南粤的旅游热点.如图,游客从某旅游景区的景点![]() 处下山至
处下山至![]() 处有两种路径,一种是从
处有两种路径,一种是从![]() 沿直线步行到
沿直线步行到![]() ,另一种是先从
,另一种是先从![]() 乘景区观光车到
乘景区观光车到![]() ,然后从
,然后从![]() 沿直线步行到
沿直线步行到![]() .现有甲、乙两位游客从
.现有甲、乙两位游客从![]() 处下山,甲沿
处下山,甲沿![]() 匀速步行,速度为50米/分钟,在甲出发2分钟后,乙从
匀速步行,速度为50米/分钟,在甲出发2分钟后,乙从![]() 乘观光车到
乘观光车到![]() ,在
,在![]() 处停留20分钟后,再从
处停留20分钟后,再从![]() 匀速步行到
匀速步行到![]() .假设观光车匀速直线运行的速度为250米/分钟,山路
.假设观光车匀速直线运行的速度为250米/分钟,山路![]() 长为2340米,经测量,
长为2340米,经测量,![]() ,
,![]() .
.
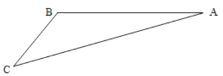
(1)求观光车路线![]() 的长;
的长;
(2)问乙出发多少分钟后,乙在观光车上与甲的距离最短?
(3)为使两位游客在![]() 处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?
处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A. φ∈R,函数f(x)=sin(2x+φ)都不是偶函数
B. α,β∈R,使cos(α+β)=cosα+cosβ
C. 向量a=(2,1),b=(-1,0),则a在b的方向上的投影为2
D. “|x|≤1”是“x≤1”的既不充分又不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com