
若点M是 ABC所在平面内一点,且满足:
ABC所在平面内一点,且满足: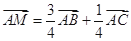 .
.
(1)求 ABM与
ABM与 ABC的面积之比.
ABC的面积之比.
(2)若N为AB中点,AM与CN交于点O,设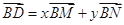 ,求
,求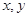 的值.
的值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
已知直线 的方向向量为
的方向向量为 ,且过点
,且过点 ,将直线
,将直线 绕着它与x轴的交点B按逆时针方向旋转一个锐角
绕着它与x轴的交点B按逆时针方向旋转一个锐角 得到直线
得到直线 ,直线
,直线 :
: .(k
.(k R).
R).
(1)求直线 和直线
和直线 的方程;
的方程;
(2)当直线 ,
, ,
, 所围成的三角形的面积为3时,求直线
所围成的三角形的面积为3时,求直线 的方程。
的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知a=(sin α,sin β),b=(cos(α-β),-1),c=(cos(α+β),2),α,β≠kπ+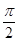 (k∈Z).
(k∈Z).
(1)若b∥c,求tan α·tan β的值;
(2)求a2+b·c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)
已知空间向量 ,
, ,
, ·
· =
= ,
, ∈(0,
∈(0, ).
).
(1)求 及
及 ,
, 的值;
的值;
(2)设函数 ,求
,求 的最小正周期和图象的对称中心坐标;
的最小正周期和图象的对称中心坐标;
(3)求函数 在区间
在区间 上的值域.
上的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com