
| 2 |
| 6 |
| 6 |
| 6 |
| 2 |
| 2 |
| ||
| 2 |
| 2 |
| π |
| 4 |
| 6 |
| 6 |
| 6 |
| 6 |
| 6 |
| 2 |
| 2 |
| sinB |
| cosB |
| ||
| 3 |
| π |
| 6 |
| 2 |
| 2 |
| 2 |
| π |
| 6 |
| ||
| 2 |
| π |
| 4 |
| 2 |
| 5π |
| 12 |
| ||||
| 4 |
| 1 |
| 2 |
| 5π |
| 12 |
| 1 |
| 2 |
| 2 |
| ||||
| 4 |
| ||
| 2 |


科目:高中数学 来源: 题型:
A、3±
| ||
B、-3±
| ||
C、2±
| ||
D、-2±
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、{α|α=57°+k•360°,k∈Z} |
| B、{α|α=-157°+k•360°,k∈Z} |
| C、{α|α=33°+k•360°,k∈Z} |
| D、{α|α=-33°+k•360°,k∈Z} |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| A、{x|1<x<2} | ||
| B、{x|-1<x<2} | ||
C、{x|
| ||
| D、{x|-1<x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:
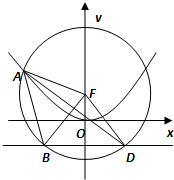 设抛物线C:x2=2py(p>0)的焦点为F,准线为l,A为C上一点,已知以F为圆心,FA为半径的圆F交l于B,D两点.若∠BFD=90°,△ABD的面积为4
设抛物线C:x2=2py(p>0)的焦点为F,准线为l,A为C上一点,已知以F为圆心,FA为半径的圆F交l于B,D两点.若∠BFD=90°,△ABD的面积为4| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩共分五组,得到频率分布表如下表所示.
某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩共分五组,得到频率分布表如下表所示.| 组号 | 分组 | 频数 | 频率 |
| 第一组 | [160,165) | 5 | 0.05 |
| 第二组 | [165,170) | 35 | 0.35 |
| 第三组 | [170,175) | 30 | ① |
| 第四组 | [175,180) | ② | 0.2 |
| 第五组 | [180,185) | 10 | 0.1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com