
【题目】已知定义在R上的函数f(x)满足条件f(x+4)=﹣f(x),且函数y=f(x+2)是偶函数,当x∈(0,2]时, ![]() ,当x∈[﹣2,0)时,f(x)的最小值为3,则a的值等于( )
,当x∈[﹣2,0)时,f(x)的最小值为3,则a的值等于( )
A.e2
B.e
C.2
D.1
【答案】A
【解析】解:∵f(x+2)是偶函数,∴f(x+2)=f(﹣x+2),
∴f(x)关于直线x=2对称,
∴当2≤x<4时,f(x)=f(4﹣x)=ln(4﹣x)﹣a(4﹣x).
∵f(x+4)=﹣f(x),
∴当﹣2≤x<0时,f(x)=﹣f(x+4)=﹣ln[4﹣(x+4)]+a[4﹣(x+4)]=﹣ln(﹣x)﹣ax,
∴f′(x)=﹣ ![]() ﹣a,
﹣a,
令f′(x)=0得x=﹣ ![]() ,
,
∵a ![]() ,∴﹣
,∴﹣ ![]() ∈(﹣2,0),
∈(﹣2,0),
∴当﹣2≤x<﹣ ![]() 时,f′(x)<0,当﹣
时,f′(x)<0,当﹣ ![]() <x<0时,f′(x)>0,
<x<0时,f′(x)>0,
∴f(x)在[﹣2,﹣ ![]() )上单调递减,在(﹣
)上单调递减,在(﹣ ![]() ,0)上单调递增,
,0)上单调递增,
∴当x=﹣ ![]() 时,f(x)取得最小值f(﹣
时,f(x)取得最小值f(﹣ ![]() )=﹣ln
)=﹣ln ![]() +1,
+1,
∵f(x)在[﹣2,0)上有最小值3,
∴﹣ln( ![]() )+1=3,解得a=e2.
)+1=3,解得a=e2.
故选A.


科目:高中数学 来源: 题型:
【题目】给出下列命题:
①x∈R,不等式x2+2x>4x-3均成立;
②若log2x+logx2≥2,则x>1;
③“若a>b>0且c<0,则 ![]() ”的逆否命题;
”的逆否命题;
④若p且q为假命题,则p,q均为假命题.
其中真命题是( )
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知非零平面向量 ![]() ,
, ![]() ,则“|
,则“| ![]() |=|
|=| ![]() |+|
|+| ![]() |”是“存在非零实数λ,使
|”是“存在非零实数λ,使 ![]() =λ
=λ ![]() ”的( )
”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在吸烟与患肺癌这两个分类变量的独立性检验的计算中,下列说法正确的是( )
A.若 ![]() 的观测值为
的观测值为 ![]() ,在犯错误的概率不超过
,在犯错误的概率不超过 ![]() 的前提下认为吸烟与患肺癌有关系,那么在100个吸烟的人中必有99人患有肺癌.
的前提下认为吸烟与患肺癌有关系,那么在100个吸烟的人中必有99人患有肺癌.
B.由独立性检验可知,在犯错误的概率不超过 ![]() 的前提下认为吸烟与患肺癌有关系时,我们说某人吸烟,那么他有
的前提下认为吸烟与患肺癌有关系时,我们说某人吸烟,那么他有 ![]() 的可能患有肺癌.
的可能患有肺癌.
C.若从统计量中求出在犯错误的概率不超过 ![]() 的前提下认为吸烟与患肺癌有关系,是指有
的前提下认为吸烟与患肺癌有关系,是指有 ![]() 的可能性使得判断出现错误.
的可能性使得判断出现错误.
D.以上三种说法都不正确.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)= 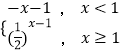 的图象与函数g(x)=log2(x+a)(a∈R)的图象恰有一个交点,则实数a的取值范围是( )
的图象与函数g(x)=log2(x+a)(a∈R)的图象恰有一个交点,则实数a的取值范围是( )
A.a>1
B.a≤﹣ ![]()
C.a≥1或a<﹣ ![]()
D.a>1或a≤﹣ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A是双曲线 ![]() 的右顶点,F(c,0)是右焦点,若抛物线
的右顶点,F(c,0)是右焦点,若抛物线 ![]() 的准线l上存在一点P,使∠APF=30°,则双曲线的离心率的范围是( )
的准线l上存在一点P,使∠APF=30°,则双曲线的离心率的范围是( )
A.[2,+∞)
B.(1,2]
C.(1,3]
D.[3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中 ![]() 中,曲线
中,曲线 ![]() 的参数方程为
的参数方程为 ![]() 为参数,
为参数, ![]() ). 以坐标原点为极点,
). 以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,已知直线
轴正半轴为极轴建立极坐标系,已知直线 ![]() 的极坐标方程为
的极坐标方程为 ![]() .
.
(1)设 ![]() 是曲线
是曲线 ![]() 上的一个动点,当
上的一个动点,当 ![]() 时,求点
时,求点 ![]() 到直线
到直线 ![]() 的距离的最大值;
的距离的最大值;
(2)若曲线 ![]() 上所有的点均在直线
上所有的点均在直线 ![]() 的右下方,求
的右下方,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在一个坡度一定的山坡AC的顶上有一高度为25m的建筑物CD,为了测量该山坡相对于水平地面的坡角θ,在山坡的A处测得∠DAC=15°,沿山坡前进50m到达B处,又测得∠DBC=45°,根据以上数据可得cosθ= . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com