
【题目】已知点![]() 及圆
及圆![]() :
: ![]() .
.
(1)若直线![]() 过点
过点![]() 且与圆心
且与圆心![]() 的距离为
的距离为![]() ,求直线
,求直线![]() 的方程.
的方程.
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() ,
, ![]() 两点,是否存在实数
两点,是否存在实数![]() ,使得过点
,使得过点![]() 的直线
的直线![]() 垂直平分弦
垂直平分弦![]() ?若存在,求出实数
?若存在,求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】试题分析:(1)当直线斜率存在时,设出直线方程,利用圆心到直线的距离等于![]() 建立方程,解出子线的斜率,由此求得直线方程.当直线斜率不存在时,直线方程为
建立方程,解出子线的斜率,由此求得直线方程.当直线斜率不存在时,直线方程为![]() ,经验证可知也符合.(2)将直线方程代入圆的方程,利用判别式大于零求得
,经验证可知也符合.(2)将直线方程代入圆的方程,利用判别式大于零求得![]() 的取值范围,利用”圆的弦的垂直平分线经过圆心”,求出直线的斜率,进而求得
的取值范围,利用”圆的弦的垂直平分线经过圆心”,求出直线的斜率,进而求得![]() 的值,由此判断
的值,由此判断![]() 不存在.
不存在.
试题解析:
(1)设直线l的斜率为k(k存在),则方程为y-0=k(x-2),即kx-y-2k=0.
又圆C的圆心为(3,-2),半径r=3,
由![]() =1,解得k=-
=1,解得k=-![]() .
.
所以直线方程为![]() ,即3x+4y-6=0.
,即3x+4y-6=0.
当l的斜率不存在时,l的方程为x=2,经验证x=2也满足条件
(2)把直线y=ax+1代入圆C的方程,消去y,整理得(a2+1)x2+6(a-1)x+9=0.
由于直线ax-y+1=0交圆C于A,B两点,
故Δ=36(a-1)2-36(a2+1)>0,
解得a<0.
则实数a的取值范围是(-∞,0).
设符合条件的实数a存在.
由于l2垂直平分弦AB,故圆心C(3,-2)必在l2上.所以l2的斜率kPC=-2.
而kAB=a=-![]() ,所以a=
,所以a=![]() .
.
由于![]() ,故不存在实数a,使得过点P(2,0)的直线l2垂直平分弦AB
,故不存在实数a,使得过点P(2,0)的直线l2垂直平分弦AB


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某加油站20名员工日销售量的频率分布直方图,如图所示:
(1)补全该频率分布直方图在[20,30)的部分,并分别计算日销售量在 [10,20),[20,30)的员工数;
(2)在日销量为[10,30)的员工中随机抽取2人,求这两名员工日销量在 [20,30)的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() .
.
(1)若直线![]() 与直线
与直线![]() 平行,求实数
平行,求实数![]() 的值;
的值;
(2)若![]() ,
, ![]() ,点
,点![]() 在直线
在直线![]() 上,已知
上,已知![]() 的中点在
的中点在![]() 轴上,求点
轴上,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)根据两直线平行,对应方向向量共线,列方程即可求出![]() 的值;(2)根据
的值;(2)根据![]() 时,直线
时,直线![]() 的方程设出点
的方程设出点![]() 的坐标,由此求出
的坐标,由此求出![]() 的中点坐标,再由中点在
的中点坐标,再由中点在![]() 轴上求出点
轴上求出点![]() 的坐标.
的坐标.
试题解析:(1)∵直线![]() 与直线
与直线![]() 平行,
平行,
∴![]() ,
,
∴![]() ,经检验知,满足题意.
,经检验知,满足题意.
(2)由题意可知: ![]() ,
,
设![]() ,则
,则![]() 的中点为
的中点为![]() ,
,
∵![]() 的中点在
的中点在![]() 轴上,∴
轴上,∴![]() ,
,
∴![]() .
.
【题型】解答题
【结束】
16
【题目】在平面直角坐标系xOy中,已知△ABC三个顶点坐标为A(7,8),B(10,4),C(2,-4).
(1)求BC边上的中线所在直线的方程;
(2)求BC边上的高所在直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,an=cos ![]() (n∈N*)
(n∈N*)
(1)试将an+1表示为an的函数关系式;
(2)若数列{bn}满足bn=1﹣ ![]() (n∈N*),猜想an与bn的大小关系,并证明你的结论.
(n∈N*),猜想an与bn的大小关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆 ![]() +
+ ![]() =1(a>b>0)的离心率为e,D为右准线上一点.
=1(a>b>0)的离心率为e,D为右准线上一点.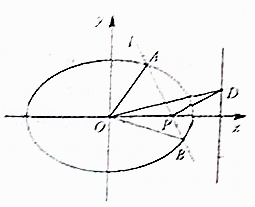
(1)若e= ![]() ,点D的横坐标为4,求椭圆的方程;
,点D的横坐标为4,求椭圆的方程;
(2)设斜率存在的直线l经过点P( ![]() ,0),且与椭圆交于A,B两点.若
,0),且与椭圆交于A,B两点.若 ![]() +
+ ![]() =
= ![]() ,DP⊥l,求椭圆离心率e.
,DP⊥l,求椭圆离心率e.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com