练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．已知等差数列{an}的a1=-20，公差为d，前n项和为Sn，则“3＜d＜5”是“Sn的最小值仅为S6”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    分析 利用Sn的最小值仅为S6，可得a6＜0，a7＞0，求出$\frac{10}{3}$＜d＜4，根据集合的包含关系判断即可．

    解答 解：∵Sn的最小值仅为S6，
    ∴a6＜0，a7＞0，
    ∴$\left\{\begin{array}{l}{-20+5d＜0}\\{-20+6d＞0}\end{array}\right.$，
    ∴$\frac{10}{3}$＜d＜4，
    3＜d＜5”是$\frac{10}{3}$＜d＜4的必要不充分条件，
    故选：B．

    点评 本题考查等差数列前n项和的最值，考查集合的包含关系以及分析解决问题的能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    5．以下判断正确的序号是（2）（3）（4）
    （1）函数y=f（x）为R上的可导函数，则f′（x0）=0是x0为函数f（x）极值点的充要条件．
    （2）$\int_0^4{（|x-1|+|x-3|）}dx$=10．
    （3）已知函数f（x）=x3+x，对任意的m∈[-2，2]，f（mx-2）+f（x）＜0恒成立，则x的取值范围为（-2，$\frac{2}{3}$）．
    （4）设f1（x）=cosx，定义fn+1（x）为fn（x）的导数，即fn+1（x）=f′n（x）n∈N，若△ABC的内角A满足${f_1}（A）+{f_2}（A）+…+{f_{2014}}（A）=\frac{1}{3}$，则sin2A=$\frac{8}{9}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．设x＞0，由不等式x+$\frac{1}{x}$≥2，x+$\frac{4}{{x}^{2}}$≥3，x+$\frac{27}{{x}^{3}}$≥4，…，推广到x+$\frac{a}{{x}^{n}}$≥n+1，则a=（　　）
    A．2nB．2nC．n2D．nn

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知直线l的参数方程为$\left\{\begin{array}{l}{x=tcosα}\\{y=1+tsinα}\end{array}\right.$（0≤α＜π，t为参数），曲线C的极坐标方程为ρ=$\frac{4cosθ}{si{n}^{2}θ}$．
    （Ⅰ）将曲线C的极坐标方程化为直角坐标方程，并说明曲线C的形状；
    （Ⅱ）若直线l经过点（1，0），求直线l被曲线C截得的线段AB的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

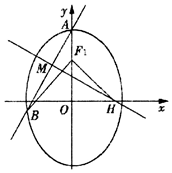    10．已知椭圆C：$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1（{a＞b＞0}）$的上、下焦点分别为F1，F2，上焦点F1到直线 4x+3y+12=0的距离为3，椭圆C的离心率e=$\frac{1}{2}$．
    （I）若P是椭圆C上任意一点，求|${\overrightarrow{P{F_1}}}$||${\overrightarrow{P{F_2}}}$|的取值范围；
    （II）设过椭圆C的上顶点A的直线l与椭圆交于点B（B不在y轴上），垂直于l的直线与l交于点M，与x轴交于点H，若$\overrightarrow{{F_1}B}•\overrightarrow{{F_1}H}$=0，且|${\overrightarrow{MO}}$|=|${\overrightarrow{MA}}$|，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．已知下列命题：
    ①?x∈（0，2），3x＞x3的否定是：?x∈（0，2），3x≤x3；
    ②若f（x）=2x-2-x，则?x∈R，f（-x）=-f（x）；
    ③若f（x）=x+$\frac{1}{x+1}$，?x0∈（0，+∞），f（x0）=1；
    ④在△ABC中，若A＞B，则sin A＞sin B．
    其中真命题是①②④．（将所有真命题序号都填上）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．下列命题中正确的是（　　）
    A．命题“?x0∈R，sinx0＞1”的否定是“?x∈R，sinx＞1”
    B．“若xy=0，则x=0或y=0”的逆否命题为“若x≠0或y≠0，则xy≠0”
    C．在△ABC中，A＞B是sinA＞sinB的充分不必要条件
    D．若p∧（￢q）为假，p∨（￢q）为真，则p，q同真或同假

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

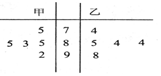    4．如图是某班甲、乙两位同学在5次阶段性检测中的数学成绩（百分制）的茎叶图，甲、乙两位同学得分的中位数分别为x1，x2，得分的方差分别为y1，y2，则下列结论正确的是（　　）
    A．x1＜x2，y1＜y2B．x1＜x2，y1＞y2C．x1＞x2，y1＞y2D．x1＞x2，y1＜y2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知函数f（x）=lnx+x2+x．正实数x1，x2满足f（x1）+f（x2）+x1x2=0，则下述结论中正确的一项是（　　）
    A．x1+x2≥$\frac{\sqrt{5}-1}{2}$B．x1+x2＜$\frac{\sqrt{5}-1}{2}$C．x1+x2≥$\frac{\sqrt{5}+1}{2}$D．x1+x2＜$\frac{\sqrt{5}+1}{2}$

    查看答案和解析>>

    同步练习册答案