已知函数f(x)=x3+mx2+nx-2的图象过点(-1,-6),且函数g(x)=f′(x)+6x是偶函数.
(Ⅰ)求m、n的值;
(Ⅱ)若a>0,求函数y=f(x)在区间(a-1,a+1)内的极值.
解:(Ⅰ)由函数f(x)图象过点(-1,-6),得m-n=-3,①…(1分)
由f(x)=x
3+mx
2+nx-2,得f′(x)=3x
2+2mx+n,…(2分)
则g(x)=f′(x)+6x=3x
2+(6+2m)x+n;
而g(x)图象关于y轴对称,所以-
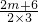
=0,所以m=-3,
代入①得n=0.…(4分)
(Ⅱ)由(Ⅰ)得f′(x)=3x(x-2),
令f′(x)=0得x=0或x=2.…(5分)
当x变化时,f′(x)、f(x)的变化情况如下表:
| x | (-∞,0) | 0 | (0,2) | 2 | …(8分)
(2,+∞) |
| f′(x) | + | 0 | - | 0 | |
| f(x) | | 极大值 | | 极小值 | |
由此可得:
当0<a<1时,f(x)在(a-1,a+1)内有极大值f(0)=-2,无极小值;
当a=1时,f(x)在(a-1,a+1)内无极值;
当1<a<3时,f(x)在(a-1,a+1)内有极小值f(2)=-6,无极大值;
当a≥3时,f(x)在(a-1,a+1)内无极值.…(11分)
综上得:当0<a<1时,f(x)有极大值-2,无极小值,当1<a<3时,有极小值-6,无极大值,当a=1或a≥3时,f(x)无极值.…(12分)
分析:(Ⅰ)利用条件的到两个关于m、n的方程,求出m、n的值即可.
(Ⅱ)利用(Ⅰ)的结论,再找函数y=f(x)的导函数大于0和小于0对应的区间,最后分情况讨论区间(a-1,a+1)和单调区间的位置关系再得结论.
点评:本小题主要考查函数的奇偶性、单调性、极值、导数、不等式等基础知识,考查运用导数研究函数性质的方法,以及分类与整合、转化与化归等数学思想方法,考查分析问题和解决问题的能力.

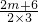 =0,所以m=-3,
=0,所以m=-3,

 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<