
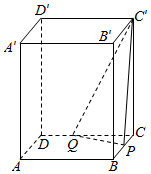
 如图,在长方体ABCD一A′B′C′D′中,点P,Q分别是棱BC,CD上的动点,BC=4,CD=3,CC′=2$\sqrt{3}$,直线CC′与平面PQC′所成的角为30°,则△PQC′的面积的最小值是( )
如图,在长方体ABCD一A′B′C′D′中,点P,Q分别是棱BC,CD上的动点,BC=4,CD=3,CC′=2$\sqrt{3}$,直线CC′与平面PQC′所成的角为30°,则△PQC′的面积的最小值是( )| A. | $\frac{18\sqrt{5}}{5}$ | B. | 8 | C. | $\frac{16\sqrt{3}}{3}$ | D. | 10 |
分析 以C为原点建立空间直角坐标系,设P(0,a,0),Q(b,0,0),求出平面PQC′的法向量$\overrightarrow{n}$,则cos<$\overrightarrow{n},\overrightarrow{CC′}$>=$\frac{1}{2}$,解出a,b的关系式,得出△PQC的最小值,又C到平面PQC′的距离为$\sqrt{3}$,利用等体积法求出△PQC′的面积最小值.
解答  解:以C为原点,以CD,CB,CC′为坐标轴建立空间直角坐标系,如图所示:
解:以C为原点,以CD,CB,CC′为坐标轴建立空间直角坐标系,如图所示:
则C(0,0,0),C′(0,0,2$\sqrt{3}$).设P(0,a,0),Q(b,0,0),于是0<a≤4,0<b≤3.
∴$\overrightarrow{QC′}$=(-b,0,2$\sqrt{3}$),$\overrightarrow{PC′}$=(0,-a,2$\sqrt{3}$),$\overrightarrow{CC′}$=(0,0,2$\sqrt{3}$),
设平面PQC′的一个法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PC′}=0}\\{\overrightarrow{n}•\overrightarrow{QC′}=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{-ay+2\sqrt{3}z=0}\\{-bx+2\sqrt{3}z=0}\end{array}\right.$,令z=1,得$\overrightarrow{n}$=($\frac{2\sqrt{3}}{b}$,$\frac{2\sqrt{3}}{a}$,1).
∴$\overrightarrow{n}•\overrightarrow{CC′}$=2$\sqrt{3}$,|$\overrightarrow{CC′}$|=2$\sqrt{3}$,|$\overrightarrow{n}$|=$\sqrt{\frac{12}{{b}^{2}}+\frac{12}{{a}^{2}}+1}$,
∴cos<$\overrightarrow{n},\overrightarrow{CC′}$>=$\frac{1}{\sqrt{\frac{12}{{b}^{2}}+\frac{12}{{a}^{2}}+1}}$=$\frac{1}{2}$.
∴$\frac{12}{{a}^{2}}+\frac{12}{{b}^{2}}=3$,∴a2+b2=$\frac{1}{4}{a}^{2}{b}^{2}$≥2ab,解得ab≥8.
∴当ab=8时,S△PQC=4,棱锥C′-PQC的体积最小,
∵直线CC′与平面PQC′所成的角为30°,∴C到平面PQC′的距离d=2$\sqrt{3}$×$\frac{1}{2}$=$\sqrt{3}$.
∵VC′-PQC=VC-PQC′,
∴$\frac{1}{3}×4×2\sqrt{3}$=$\frac{1}{3}×{S}_{△PQC′}×\sqrt{3}$,∴S△PQC′=8.
故选:B.
点评 本题你考查了线面角的计算,空间向量的应用,基本不等式,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
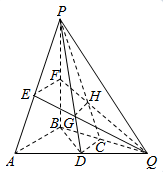 如图所示,在三棱锥P-ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连接GH.
如图所示,在三棱锥P-ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连接GH.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
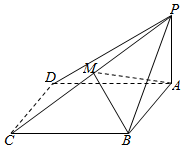 四棱锥P-ABCD中,底面ABCD为正方形,PA⊥面ABCD,PA=$\frac{1}{2}$AB.
四棱锥P-ABCD中,底面ABCD为正方形,PA⊥面ABCD,PA=$\frac{1}{2}$AB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
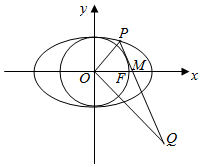 在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,右焦点F(1,0).
在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,右焦点F(1,0).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com