
分析 由已知可得:A(-a,0),B(a,0),左、右焦点分别是F1(-c,0),F2(c,0).根据|F1F2|2=λ|AF1|•|BF2|,可得λ=$\frac{4{c}^{2}}{(a-c)^{2}}$=$\frac{4{e}^{2}}{1-2e+{e}^{2}}$,利用0<λ<4,解出即可得出.
解答 解:∵A(-a,0),B(a,0),左、右焦点分别是F1(-c,0),F2(c,0).
∵|F1F2|2=λ|AF1|•|BF2|,
∴λ=$\frac{4{c}^{2}}{(a-c)^{2}}$=$\frac{4{e}^{2}}{1-2e+{e}^{2}}$,
∵0<λ<4,
∴0<$\frac{4{e}^{2}}{1-2e+{e}^{2}}$<4,0<e<1,
解得$0<e<\frac{1}{2}$.
故答案为:$(0,\frac{1}{2})$.
点评 本题考查了椭圆的标准方程及其性质、不等式的解法、方程的解法,考查了推理能力与计算能力,属于中档题.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:解答题
| 上一年的 出险次数 | 0 | 1 | 2 | 3 | 4 | 5次以上(含5次) |
| 下一年 保费倍率 | 85% | 100% | 125% | 150% | 175% | 200% |
| 连续两年没有出险打7折,连续三年没有出险打6折 | ||||||
| 一年中出险次数 | 0 | 1 | 2 | 3 | 4 | 5次以上(含5次) |
| 频数 | 500 | 380 | 100 | 15 | 4 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-1,1] | C. | [1,3) | D. | (1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,+∞) | C. | (0,+∞) | D. | (0,1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
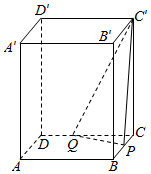 如图,在长方体ABCD一A′B′C′D′中,点P,Q分别是棱BC,CD上的动点,BC=4,CD=3,CC′=2$\sqrt{3}$,直线CC′与平面PQC′所成的角为30°,则△PQC′的面积的最小值是( )
如图,在长方体ABCD一A′B′C′D′中,点P,Q分别是棱BC,CD上的动点,BC=4,CD=3,CC′=2$\sqrt{3}$,直线CC′与平面PQC′所成的角为30°,则△PQC′的面积的最小值是( )| A. | $\frac{18\sqrt{5}}{5}$ | B. | 8 | C. | $\frac{16\sqrt{3}}{3}$ | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
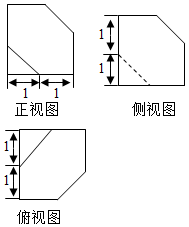
| A. | 4 | B. | 3$\sqrt{3}$+12 | C. | 21+$\sqrt{3}$ | D. | $\frac{{3\sqrt{3}}}{2}$+12 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
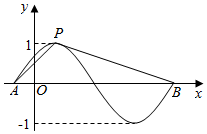 函数y=sin($\frac{π}{4}$x+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,则tan∠APB=-$\frac{8}{11}$.
函数y=sin($\frac{π}{4}$x+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,则tan∠APB=-$\frac{8}{11}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com