
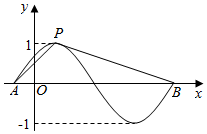
 函数y=sin($\frac{π}{4}$x+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,则tan∠APB=-$\frac{8}{11}$.
函数y=sin($\frac{π}{4}$x+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,则tan∠APB=-$\frac{8}{11}$. 分析 由条件利用正弦函数的图象特征求得AB、PA、PB的值,利用余弦定理求得cos∠APB 的值,再利用同角三角函数的基本关系求得tan∠APB的值.
解答 解:根据函数y=sin($\frac{π}{4}$x+φ)(φ>0)的部分图象,可得AB=$\frac{2π}{\frac{π}{4}}$=8,
PA=$\sqrt{1{+2}^{2}}$=$\sqrt{5}$,PB=$\sqrt{1{+6}^{2}}$=$\sqrt{37}$,
利用余弦定理可得cos∠APB=$\frac{{PA}^{2}{+PB}^{2}{-AB}^{2}}{2PA•PB}$=-$\frac{11}{\sqrt{185}}$,
∴sin∠APB=$\sqrt{{1-cos}^{2}∠AOB}$=$\frac{8}{\sqrt{185}}$,∴tan∠APB=$\frac{sin∠APB}{cos∠APB}$=-$\frac{8}{11}$,
故答案为:-$\frac{8}{11}$.
点评 本题主要考查正弦函数的图象的特征,余弦定理,同角三角函数的基本关系,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 年份200x(年) | 0 | 1 | 2 | 3 | 4 |
| 人口数 y (十万) | 5 | 7 | 8 | t | 19 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5海里 | B. | 5$\sqrt{2}$海里 | C. | 10海里 | D. | 10$\sqrt{2}$海里 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com