
【题目】下列选项中,说法正确的是( )
A.命题“![]() ,
,![]() ”的否定为“
”的否定为“![]() ,
,![]() ”;
”;
B.命题“在![]() 中,
中,![]() ,则
,则![]() ”的逆否命题为真命题;
”的逆否命题为真命题;
C.已知![]() 、m是两条不同的直线,
、m是两条不同的直线,![]() 是个平面,若
是个平面,若![]() ,则
,则![]() ;
;
D.已知定义在R上的函数![]() ,则“
,则“![]() 为奇函数”是“
为奇函数”是“![]() ”的充分必要条件.
”的充分必要条件.
【答案】C
【解析】
由特称命题的否定为全称命题,即可判断A;
由![]() ,可得
,可得![]() ,再结合原命题与逆否命题等价,即可判断B;
,再结合原命题与逆否命题等价,即可判断B;
由线面平行的性质定理,即可判断C;
根据奇函数的定义,即可判断D.
解:对于A,由特称命题的否定为全称命题,可得命题“![]() ,
,![]() ”
”
的否定为“![]() ,
,![]() ”,故A错;
”,故A错;
对于B,命题“在![]() 中,
中,![]() ,则
,则![]() ”为假命题,比如
”为假命题,比如![]() ,则
,则![]() .
.
再由原命题与其逆否命题等价,则其逆否命题为假命题,故B错;
对于C,已知![]() 、m是两条不同的直线,
、m是两条不同的直线,![]() 是个平面,若
是个平面,若![]() ,则存在
,则存在![]() ,
,![]() ,必有
,必有![]() ,又
,又![]() ,则
,则![]() ,所以
,所以![]() ,故C正确;
,故C正确;
对于D,已知定义在R上的函数![]() ,若
,若![]() 为奇函数,则
为奇函数,则![]() ,则
,则![]() ,所以
,所以![]() ,满足充分性;但
,满足充分性;但![]() 不能推出
不能推出![]() 为奇函数,不满足必要性,则“
为奇函数,不满足必要性,则“![]() 为奇函数”是“
为奇函数”是“![]() ”的充分不必要条件,故D错.
”的充分不必要条件,故D错.
故选:C.


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 、抛物线
、抛物线![]() 的焦点均在
的焦点均在![]() 轴上,
轴上,![]() 的中心和
的中心和![]() 的顶点均为原点
的顶点均为原点![]() ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:
| 3 |
| 4 |
|
|
| 0 |
|
|
(Ⅰ)求![]() 的标准方程;
的标准方程;
(Ⅱ)请问是否存在直线![]() 满足条件:①过
满足条件:①过![]() 的焦点
的焦点![]() ;②与
;②与![]() 交不同两点
交不同两点![]() 且满足
且满足![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为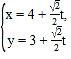 (
(![]() 为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线
为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且设定点
两点,且设定点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①线性相关系数![]() 越大,两个变量的线性相关性越强;反之,线性相关性越弱;
越大,两个变量的线性相关性越强;反之,线性相关性越弱;
②用![]() 来刻画回归效果,
来刻画回归效果,![]() 越大,说明模型的拟合效果越好;
越大,说明模型的拟合效果越好;
③根据![]() 列联表中的数据计算得出的
列联表中的数据计算得出的![]() 的值越大,两类变量相关的可能性就越大;
的值越大,两类变量相关的可能性就越大;
④在回归分析模型中,残差平方和越小,说明模型的拟合效果越好;
⑤从匀速传递的产品生产流水线上,质检员每10分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样.
其中真命题的序号是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】不期而至的新冠肺炎疫情,牵动了亿万国人的心,全国各地纷纷捐赠物资驰援武汉.有一批捐赠物资需要通过轮船沿长江运送至武汉,已知该运送物资的轮船在航行中每小时的燃料费和它的速度的立方成正比,已知当速度为10海里/时时,燃料费是6元/时,而其他与速度无关的费用是96元/时,问当轮船的速度是多少时,航行1海里所需的费用总和最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln (x+1)-![]() -x,a∈R.
-x,a∈R.
(1)当a>0时,求函数f(x)的单调区间;
(2)若存在x>0,使f(x)+x+1<-![]() (a∈Z)成立,求a的最小值.
(a∈Z)成立,求a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为![]() 的正方形
的正方形![]() 和高为
和高为![]() 的等腰梯形
的等腰梯形![]() 所在的平面互相垂直,
所在的平面互相垂直,![]() ,
,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 为线段
为线段![]() 上任意一点.
上任意一点.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)是否存在点![]() 使平面
使平面![]() 与平面
与平面![]() 垂直,若存在,求出
垂直,若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:

(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数![]() ,并将完成生产任务所需时间超过
,并将完成生产任务所需时间超过![]() 和不超过
和不超过![]() 的工人数填入下面的列联表:
的工人数填入下面的列联表:
超过 | 不超过 | |
第一种生产方式 | ||
第二种生产方式 |
(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?
附:![]() ,
,
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com