
【题目】已知函数f(x)=ln (x+1)-![]() -x,a∈R.
-x,a∈R.
(1)当a>0时,求函数f(x)的单调区间;
(2)若存在x>0,使f(x)+x+1<-![]() (a∈Z)成立,求a的最小值.
(a∈Z)成立,求a的最小值.
【答案】(1)见解析(2)5.
【解析】试题分析:(1)先求导数,转化研究二次函数![]() 符号变化规律:当判别式非正时,导函数不变号;当判别式大于零时,定义域上有两个根 ,导函数符号先负再正再负(2)先利用参变分离法化简不等式得
符号变化规律:当判别式非正时,导函数不变号;当判别式大于零时,定义域上有两个根 ,导函数符号先负再正再负(2)先利用参变分离法化简不等式得![]() ,转化求函数
,转化求函数![]() 最小值,利用导数可得
最小值,利用导数可得![]() 有唯一极小值,也是最小值,再根据极点条件求最小值取值范围,进而可得a的最小值.
有唯一极小值,也是最小值,再根据极点条件求最小值取值范围,进而可得a的最小值.
试题解析: 解 (1)f′(x)=![]() ,x>-1.
,x>-1.
当a≥![]() 时,f′(x)≤0,∴f(x)在(-1,+∞)上单调递减.
时,f′(x)≤0,∴f(x)在(-1,+∞)上单调递减.
当0<a<![]() 时,
时,
当-1<x<![]() 时,f′(x)<0,f(x)单调递减;
时,f′(x)<0,f(x)单调递减;
当![]() <x<
<x<![]() 时,f′(x)>0,f(x)单调递增;
时,f′(x)>0,f(x)单调递增;
当x>![]() 时,f′(x)<0,f(x)单调递减.
时,f′(x)<0,f(x)单调递减.
综上,当a≥![]() 时,f(x)的单调递减区间为(-1,+∞);
时,f(x)的单调递减区间为(-1,+∞);
当0<a<![]() 时,f(x)的单调递减区间为
时,f(x)的单调递减区间为![]() ,
,![]() ,
,
f(x)的单调递增区间为![]() .
.
(2)原式等价于ax>(x+1)ln (x+1)+2x+1,
即存在x>0,使![]() 成立.
成立.
设![]() ,x>0,
,x>0,
则![]() ,x>0,
,x>0,
设h(x)=x-1-ln (x+1),x>0,
则h′(x)=1-![]() >0,∴h(x)在(0,+∞)上单调递增.
>0,∴h(x)在(0,+∞)上单调递增.
又h(2)<0,h(3)>0,根据零点存在性定理,可知h(x)在(0,+∞)上有唯一零点,设该零点为x0,则x0-1=ln (x0+1),且x0∈(2,3),
∴![]()
又a>x0+2,a∈Z,∴a的最小值为5.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 为
为![]() 的中点,以
的中点,以![]() 为折痕把
为折痕把![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且二面角
的位置,且二面角![]() 为直二面角,连结
为直二面角,连结![]() .
.
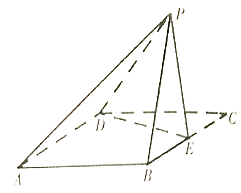
(1)记平面![]() 与平面
与平面![]() 相较于
相较于![]() ,在图中作出
,在图中作出![]() ,并说明画法;
,并说明画法;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新高考改革后,国家只统一考试数学和语文,英语学科改为参加等级考试,每年考两次,分别放在每个学年的上、下学期,物理、化学、生物、地理、历史、政治这六科则以该省的省会考成绩为准.考生从中选择三科成绩,参加大学相关院系的录取.
(1)若英语等级考试成绩有一次为优,即可达到某211院校的录取要求.假设某个学生参加每次等级考试事件是独立的,且该生英语等级考试成绩为优的概率都是![]() ,求该生在高二上学期的英语等级考试成绩才为优的概率;
,求该生在高二上学期的英语等级考试成绩才为优的概率;
(2)据预测,要想报考该211院校的相关院系,省会考的成绩至少在90分以上,才有可能被该校录取.假设该生在省会考六科的成绩,考到90分以上概率都是![]() ,设该生在省会考时考到90分以上的科目数为
,设该生在省会考时考到90分以上的科目数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市一调查机构针对该市市场占有率最高的甲、乙两家网络外卖企业以下简称外卖甲,外卖乙的经营情况进行了调查,调查结果如表:
日期 | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 |
外卖甲日接单x(百单 | 5 | 2 | 9 | 8 | 11 |
外卖乙日接单y(百单 | 2.2 | 2.3 | 10 | 5 | 15 |
(Ⅰ)据统计表明,y与x之间具有线性相关关系.经计算求得y与x之间的回归方程为![]() ,假定每单外卖业务企业平均能获纯利润3元,试预测当外卖乙日接单量不低于2500单时,外卖甲所获取的日纯利润的大致范围;(x值精确到0.01)
,假定每单外卖业务企业平均能获纯利润3元,试预测当外卖乙日接单量不低于2500单时,外卖甲所获取的日纯利润的大致范围;(x值精确到0.01)
(Ⅱ)试根据表格中这五天的日接单量情况,从平均值和方差角度说明这两家外卖企业的经营状况.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列选项中,说法正确的是( )
A.命题“![]() ,
,![]() ”的否定为“
”的否定为“![]() ,
,![]() ”;
”;
B.命题“在![]() 中,
中,![]() ,则
,则![]() ”的逆否命题为真命题;
”的逆否命题为真命题;
C.已知![]() 、m是两条不同的直线,
、m是两条不同的直线,![]() 是个平面,若
是个平面,若![]() ,则
,则![]() ;
;
D.已知定义在R上的函数![]() ,则“
,则“![]() 为奇函数”是“
为奇函数”是“![]() ”的充分必要条件.
”的充分必要条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《高中数学课程标准》(2017 版)规定了数学学科的六大核心素养.为了比较甲、乙两名高二学生的数学核心素养水平,现以六大素养为指标对二人进行了测验,根据测验结果绘制了雷达图(如图,每项指标值满分为![]() 分,分值高者为优),则下面叙述正确的是( )
分,分值高者为优),则下面叙述正确的是( )
(注:雷达图(Radar Chart),又可称为戴布拉图、蜘蛛网图(Spider Chart),可用于对研究对象的多维分析)

A.甲的数据分析素养高于乙
B.甲的数学建模素养优于数学抽象素养
C.乙的六大素养中逻辑推理最差
D.乙的六大素养整体水平优于甲
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接![]() 年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了
年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了![]() 名学生,将他们的比赛成绩(满分为
名学生,将他们的比赛成绩(满分为![]() 分)分为
分)分为![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
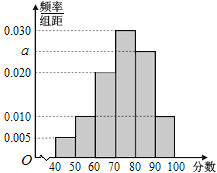
(1)求![]() 的值;
的值;
(2)记![]() 表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于
表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于![]() 分”,估计
分”,估计![]() 的概率;
的概率;
(3)在抽取的![]() 名学生中,规定:比赛成绩不低于
名学生中,规定:比赛成绩不低于![]() 分为“优秀”,比赛成绩低于
分为“优秀”,比赛成绩低于![]() 分为“非优秀”.请将下面的
分为“非优秀”.请将下面的![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为“比赛成绩是否优秀与性别有关”?
的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 |
| ||
女生 |
| ||
合计 |
|
参考公式及数据: ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在等比数列{an}中,a1=2,且a1,a2,a3-2成等差数列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足:![]() ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com