
分析 (1)由条件利用三角恒等变换化简函数f(x)的解析式,再利用正弦函数的单调性求得f(x)的单调递减区间.
(2)由条件求得$sin(x+\frac{π}{3})=\frac{4}{5}$,再利用诱导公式求得cos(x-$\frac{π}{6}$)的值,利用二倍角的余弦公公式求得$cos(2x-\frac{π}{3})$的值.
解答 解:(1)$f(x)=2cos(x+\frac{π}{6})+2sinx=2cosxcos\frac{π}{6}-2sinxsin\frac{π}{6}+2sinx$=$\sqrt{3}cosx+sinx=2sin(x+\frac{π}{3})$,
令$\frac{π}{2}+2kπ<x+\frac{π}{3}<\frac{3π}{2}+2kπ⇒\frac{π}{6}+2kπ<x<\frac{7π}{6}+2kπ$,
故f(x)的单调递减区间是$(\frac{π}{6}+2kπ,\frac{7π}{6}+2kπ),k∈Z$.
(2)由(1)得$f(x)=2sin(x+\frac{π}{3})$,由$2sin(x+\frac{π}{3})=\frac{8}{5}$,可得$sin(x+\frac{π}{3})=\frac{4}{5}$,
∵$sin(x+\frac{π}{3})=sin(\frac{π}{2}-\frac{π}{6}+x)=cos(x-\frac{π}{6})=\frac{4}{5}$,
∴$cos(2x-\frac{π}{3})=cos[2(x-\frac{π}{6})]=2{cos^2}(x-\frac{π}{6})-1=\frac{7}{25}$.
点评 本题主要考查三角恒等变换,正弦函数的单调性,诱导公式、二倍角的余弦公式的应用,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB是圆柱OO′的一条母线,BC过底面圆心O,D是圆O上一点.已知AB=BC=10,S侧=2πrh=100π.
如图,AB是圆柱OO′的一条母线,BC过底面圆心O,D是圆O上一点.已知AB=BC=10,S侧=2πrh=100π.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平均数为10,方差为2 | B. | 平均数为11,方差为3 | ||
| C. | 平均数为11,方差为2 | D. | 平均数为12,方差为4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
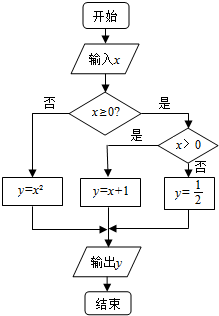
| A. | y=$\left\{\begin{array}{l}{{x}^{2},x≥0}\\{x+1,x<0}\end{array}\right.$ | B. | y=$\left\{\begin{array}{l}{\frac{1}{2},x≥0}\\{{x}^{2},x<0}\end{array}\right.$ | ||
| C. | y=$\left\{\begin{array}{l}{{x}^{2},x<0}\\{\frac{1}{2},x=0}\\{x+1,x>0}\end{array}\right.$ | D. | y=$\left\{\begin{array}{l}{{x}^{2},x>0}\\{\frac{1}{2},x=0}\\{x+1,x<0}\end{array}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
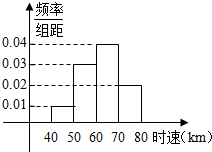
| A. | 60辆 | B. | 80辆 | C. | 70辆 | D. | 140辆 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在直角梯形ABCD中,AB∥CD,∠BAD=90°,且AB=AD=$\frac{1}{2}$CD=2,$\overrightarrow{CB}$=3$\overrightarrow{CM}$,则$\overrightarrow{DM}$•$\overrightarrow{AC}$的值为12.
如图,在直角梯形ABCD中,AB∥CD,∠BAD=90°,且AB=AD=$\frac{1}{2}$CD=2,$\overrightarrow{CB}$=3$\overrightarrow{CM}$,则$\overrightarrow{DM}$•$\overrightarrow{AC}$的值为12.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com