练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知△ABC的内角A，B，C的对边分别为a，b，c，若cosA=
    1
    3
    ，sinC=3sinB，且S△ABC=
    		2
    ，则b=（　　）
    A、1
    B、2
    		3
    C、3
    		2
    D、3
    考点：正弦定理
    专题：三角函数的求值
    分析：由cosA的值，利用同角三角函数间的基本关系求出sinA的值，利用正弦定理化简sinC=3sinB，再利用三角形面积公式列出关系式，将sinA，已知面积，以及表示出的c代入计算即可求出b的值．
    解答： 解：∵cosA=
    1
    3
    ，A为三角形内角，
    ∴sinA=
    		1-cos2A
    =
    2
    		2
    3
    ，
    由正弦定理化简sinC=3sinB，得c=3b，
    ∵S△ABC=
    1
    2
    bcsinA=
    1
    2
    3b2•
    2
    		2
    3
    =
    		2
    ，
    ∴b=1．
    故选：A．
    点评：此题考查了正弦定理，三角形面积公式，以及同角三角函数间的基本关系，熟练掌握正弦定理是解本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

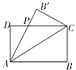    某制冷设备厂设计生产一种长方形薄板，如图所示，长方形ABCD（AB＞AD）的周长为4米，沿AC折叠使B到B′位置，AB′交DC于P．研究发现当ADP的面积最大时最节能，则最节能时长方形ABCD的面积为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知数列{an}的各项均为正数，执行程序框图（如图），当k=4时，S=
    1
    3
    ，则a2014=（　　）
    A、2012B、2013
    C、2014D、2015

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设全集U={x|0＜x＜2}，集合A={x|0＜x≤1}，则集合∁UA=（　　）
    A、（0，1）
    B、（0，1]
    C、（1，2）
    D、[1，2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    将一颗骰子连续抛掷三次，已知它落地时向上的点数恰好依次成等差数列，那么这三次抛掷向上的点数之和为12的概率为（　　）
    A、
    5
    18
    B、
    1
    9
    C、
    3
    18
    D、
    1
    72

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知直线
    		3
    x+y+m=0与圆x2+y2=9交于A，B两点，则与向量
    OA
    +
    OB
    （O为坐标原点）共线的一个向量为（　　）
    A、（1，-
    		3
    3
    ）
    B、（1，
    		3
    3
    ）
    C、（1，
    		3
    ）
    D、（1，-
    		3
    ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，矩形ABCD和矩形ABEF中，矩形ABEF可沿AB任意翻折，AF=AD，M、N分别在AE、DB上运动，当F、A、D不共线，M、N不与A、D重合，且AM=DN时，有（　　）
    A、MN∥平面FAD
    B、MN与平面FAD相交
    C、MN⊥平面FAD
    D、MN与平面FAD可能平行，也可能相交

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列叙述中，正确的个数是（　　）
    ①命题p：“?x∈R，x2-2≥0”的否定形式为￢p：“?x∈R，x2-2＜0”；
    ②O是△ABC所在平面上一点，若
    OA
    •
    OB
    =
    OB
    •
    OC
    =
    OC
    •
    OA
    ，则O是△ABC的垂心；
    ③“M＞N”是“（
    2
    3
    ）M＞（
    2
    3
    ）N”的充分不必要条件；
    ④命题“若x2-3x-4=0，则x=4”的逆否命题为“若x≠4，则x2-3x-4≠0”；
    ⑤已知
    a
    =（2，-1），
    b
    =（m，m-1），则
    a
    和
    b
    的夹角为锐角充要条件为：m＞-1．
    A、1B、2C、3D、4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    把一颗骰子投掷两次，观察出现的点数，并记第一次出现的点数为a，第二次出现的点数为b．试就方程组
    ax+by=3
    x+2y=2
    解答下列问题：
    （Ⅰ）求方程组没有解的概率；
    （Ⅱ）求以方程组的解为坐标的点在第四象限的概率．

    查看答案和解析>>

    同步练习册答案