
分析 根据正弦定理把△ABC外接圆R与三角形内角和边长建立关系,即可求出△ABC的面积.
解答 解:由△ABC外接圆的面积为4π,
∴半径R=2.
由正弦定理:$\frac{a}{sinA}$=$\frac{b}{sinB}$=2R,
则有$\frac{4}{sinB}=\frac{a}{sin60°}=4$.
可得:sinB=1,即B=$\frac{π}{2}$.
a=2$\sqrt{3}$.
勾股定理可得:c=2.
△ABC的面积S=$\frac{1}{2}$ac=2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 本题考查三角形的正弦定理的运用,考查运算能力,属于基础题.


科目:高中数学 来源: 题型:解答题
 如图,长方体ABCD-A1B1C1D1中,点M在棱BB1上,两条直线MA,MC与平面ABCD所成角均为θ,AC与BD交于点O.
如图,长方体ABCD-A1B1C1D1中,点M在棱BB1上,两条直线MA,MC与平面ABCD所成角均为θ,AC与BD交于点O.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
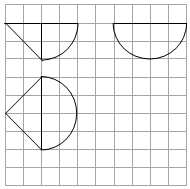 某组合体的三视图如图所示,图中网格每个小正方形的边长为1,曲线均为圆弧的一部分,则该几何体的体积为( )
某组合体的三视图如图所示,图中网格每个小正方形的边长为1,曲线均为圆弧的一部分,则该几何体的体积为( )| A. | $\frac{28}{3}π$ | B. | 4π | C. | $\frac{10}{3}π$ | D. | $\frac{2}{3}+\frac{8}{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 0 | 1 | 3 | 4 |
| y | 22 | 35 | 48 | 75 |
| A. | 22 | B. | 26 | C. | 33.6 | D. | 19.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3π}{4}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{6}$ | D. | $\frac{3π}{4}$或$\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M=N | B. | M?N | C. | M?N | D. | M∩N=∅ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com