
已知四面体的三组对棱分别相等,且长分别为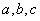 ,则此四面体的外接球的表面积为 .
,则此四面体的外接球的表面积为 .
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:
观察分析下表中的数据:猜想一般凸多面体中F,V,E所满足的等 式是________.
式是________.
| 多面体 | 面数(F) | 顶点数(V) | 棱数(E) |
| 三棱柱 | 5 | 6 | 9 |
| 五棱锥 | 6 | 6 | 10 |
| 立方体 | 6 | 8 | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com