
某地区因干旱缺水,政府向市民宣传节约用水,并进行广泛动员 三个月后,统计部门在一个小区随机抽取了 户家庭,分别调查了他们在政府动员前后三个月的月平均用水量(单位:吨),将所得数据分组,画出频率分布直方图(如图所示)
户家庭,分别调查了他们在政府动员前后三个月的月平均用水量(单位:吨),将所得数据分组,画出频率分布直方图(如图所示)

动员前 动员后
(Ⅰ)已知该小区共有居民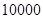 户,在政府进行节水动员前平均每月用水量是
户,在政府进行节水动员前平均每月用水量是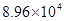 吨,请估计该小区在政府动员后比动员前平均每月节约用水多少吨;
吨,请估计该小区在政府动员后比动员前平均每月节约用水多少吨;
(Ⅱ)为了解动员前后市民的节水情况,媒体计划在上述家庭中,从政府动员前月均用水量在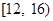 范围内的家庭中选出
范围内的家庭中选出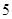 户作为采访对象,其中在
户作为采访对象,其中在 内的抽到
内的抽到 户,求
户,求 的分布列和期望
的分布列和期望
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
一中食堂有一个面食窗口,假设学生买饭所需的时间互相独立,且都是整数分钟,对以往学生买饭所需的时间统计结果如下:
| 买饭时间(分) | 1 | 2 | 3 | 4 | 5 |
| 频率 | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
袋中有8个大小相同的小球,其中1个黑球,3个白球,4个红球.
(I)若从袋中一次摸出2个小球,求恰为异色球的概率;
(II)若从袋中一次摸出3个小球,且3个球中,黑球与白球的个数都没有超过红球的个数,记此时红球的个数为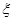 ,求
,求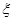 的分布列及数学期望E
的分布列及数学期望E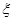 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)一批产品需要进行质量检验,检验方案是:先从这批产品中任取4件作检验,这4件产品中优质品的件数记为n。如果n=3,再从这批产品中任取4件作检验,若都为优质品,则这批产品通过检验;如果n=4,再从这批产品中任取1件作检验,若为优质品,则这批产品通过检验;其他情况下,这批产品都不能通过检验。
假设这批产品的优质品率为50%,即取出的产品是优质品的概率都为,且各件产品是否为优质品相互独立
(1)求这批产品通过检验的概率;
(2)已知每件产品检验费用为100元,凡抽取的每件产品都需要检验,对这批产品作质量检验所需的费用记为X(单位:元),求X的分布列及数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了更好地开展社团活动,丰富同学们的课余生活,现用分层抽样的方法从“模拟联合国”,“街舞”,“动漫”,“话剧”四个社团中抽取若干人组成社团指导小组,有关数据见下表:(单位:人)
(1)求 的值;
的值;
(2)若从“动漫”与“话剧”社团已抽取的人中选2人担任指导小组组长,求这2人分别来自这两个社团的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
小明参加完高考后,某日路过一家电子游戏室,注意到一台电子游戏机的规则是:你可在1,2,3,4,5,6点中选一个,押上赌注a元。掷3枚骰子,如果所押的点数出现1次、2次、3次,那么原来的赌注仍还给你,并且你还分别可以收到赌注的1倍、2倍、3倍的奖励。如果所押的点数不出现,那么赌注就被庄家没收。
(1)求掷3枚骰子,至少出现1枚为1点的概率;
(2)如果小明准备尝试一次,请你计算一下他获利的期望值,并给小明一个正确的建议。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
德阳中学数学竞赛培训共开设有初等代数、初等几何、初等数论和微积分初步共四门课程,要求初等代数、初等几何都要合格,且初等数论和微积分初步至少有一门合格,则能取得参加数学竞赛复赛的资格,现有甲、乙、丙三位同学报名参加数学竞赛培训,每一位同学对这四门课程考试是否合格相互独立,其合格的概率均相同,(见下表),且每一门课程是否合格相互独立,
| 课 程 | 初等代数 | 初等几何 | 初等数论 | 微积分初步 |
| 合格的概率 |  |  |  |  |
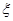 表示三位同学中取得参加数学竞赛复赛的资格的人数,求
表示三位同学中取得参加数学竞赛复赛的资格的人数,求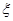 的分布列及期望
的分布列及期望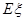 .
.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
节日期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段 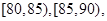
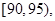
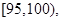
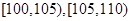 后得到如下图的频率分布直方图.
后得到如下图的频率分布直方图.
(1)此调查公司在采样中,用到的是什么抽样方法?
(2)求这40辆小型车辆车速的众数和中位数的估计值;
(3)若从车速在 的车辆中任抽取2辆,求抽出的2辆车中车速在
的车辆中任抽取2辆,求抽出的2辆车中车速在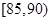 的车辆数
的车辆数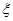 的分布列及数学期望.
的分布列及数学期望.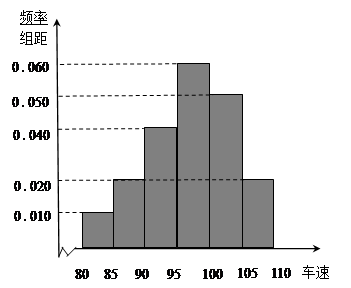
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com