
分析 (1)根据平面向量的数量积公式,结合降幂公式(二倍角公式逆用)及辅助角公式,我们易将函数的解析式化为正弦型函数的形式,进而根据正弦型函数的性质,我们可以求出函数的单调增区间及对称中心,
(2)先求出A的值,再根据三角形的面积和余弦定理即可求出.
解答 解:(1)f(x)=$\sqrt{3}sin2x-2{cos^2}x-1$=$\sqrt{3}sin2x-cos2x-2$=$2sin({2x-\frac{π}{6}})-2$,
令$2kπ-\frac{π}{2}≤2x-\frac{π}{6}≤2kπ+\frac{π}{2}$,得$kπ-\frac{π}{6}≤x≤kπ+\frac{π}{3},k∈Z$,
所以f(x)的单调增区间是$[{kπ-\frac{π}{6},kπ+\frac{π}{3}}],k∈Z$.
令$2x-\frac{π}{6}=kπ$,可得$x=\frac{π}{12}+\frac{1}{2}kπ,k∈Z$,
所以函数f(x)的对称中心为$({\frac{π}{12}+\frac{1}{2}kπ,-2})(k∈Z)$.
(2)∵f(A)=$2sin({2A-\frac{π}{6}})-2=0$,
∴$sin({2A-\frac{π}{6}})=1$,
∵A∈(0,π)
∴$2A-\frac{π}{6}∈(-\frac{π}{6},\frac{11π}{6})$,
∴$2A-\frac{π}{6}=\frac{π}{2},A=\frac{π}{3}$,
∵${S_{△ABC}}=\frac{1}{2}bcsinA=\frac{{\sqrt{3}}}{4}bc=\sqrt{3},b=1$,
∴c=4,
由余弦定理${a^2}={b^2}+{c^2}-2bccosA=1+16-2×1×4×\frac{1}{2}=13$,
∴$a=\sqrt{13}$.
点评 本题考查的知识点是平面向量的数量积运算,正弦型函数的图象和性,以及三角形的面积公式和余弦定理,属于中档题


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -1 | C. | 2 | D. | $-1或\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 模拟实验次数 |
| A | 甲 | 2次 | 6次 | 4次 | 12次 |
| B | 乙 | 3次 | 6次 | 3次 | 12次 |
| C | 丙 | 2次 | 2次 | 8次 | 12次 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
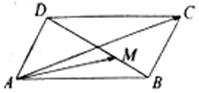 如图,平行四边形ABCD中,AB=2,AD=1,∠DAB=60°,$\overrightarrow{DM}=2\overrightarrow{MB}$,则$\overrightarrow{AC}•\overrightarrow{AM}$=4.
如图,平行四边形ABCD中,AB=2,AD=1,∠DAB=60°,$\overrightarrow{DM}=2\overrightarrow{MB}$,则$\overrightarrow{AC}•\overrightarrow{AM}$=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,-\frac{1}{4})$ | B. | $(-\frac{1}{4},+∞)$ | C. | (0,+∞) | D. | (-∞,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com