
(本小题满分12分)如图所示,在长方体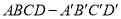 中,
中,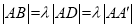 ,(
,(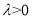 ),
),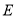 、
、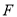 分别是
分别是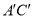 和
和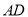 的中点,且
的中点,且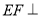 平面
平面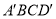 .
.

(1)求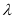 的值;
的值;
(2)求二面角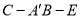 的余弦值.
的余弦值.
(1)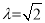 ;(2)
;(2)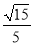 .
.
【解析】
试题分析:(1)分析题意,以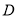 为原点,
为原点,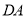 ,
,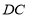 ,
,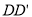 的方向分别作为
的方向分别作为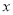 ,
,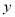 ,
,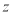 轴的正方向建立空间直角坐标系,分别求出
轴的正方向建立空间直角坐标系,分别求出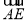 ,
,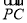 的坐标,计算向量的数量积,求得
的坐标,计算向量的数量积,求得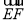 ,
,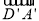 ,
,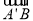 ,则由条件可知
,则由条件可知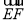 是平面
是平面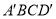 的法向量,利用
的法向量,利用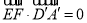 ,
,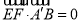 即可求得
即可求得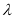 的值;(2)分别求出平面
的值;(2)分别求出平面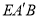 与平面
与平面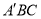 的一个法向量,利用法向量即可求得二面角
的一个法向量,利用法向量即可求得二面角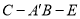 的余弦值.
的余弦值.
试题解析:以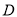 为原点,
为原点,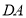 ,
,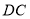 ,
,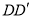 为
为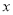 ,
,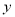 ,
, 轴的正方向建立空间直角坐标系,设
轴的正方向建立空间直角坐标系,设 ,则
,则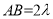 ,则
,则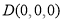 ,
, ,
,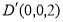 ,
,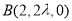 ,
,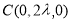 ,
,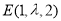 ,
,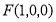 , 2分
, 2分
(1)由已知可得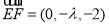 ,
,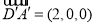 ,
,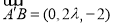 , 3分
, 3分
∵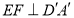 ,
,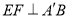 ,∴
,∴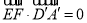 ,
,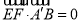 , 4分
, 4分
即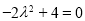 ,∴
,∴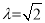 ; 5分
; 5分
(2)设平面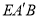 的法向量为
的法向量为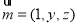 ,则
,则 ,
,
∵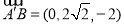 ,
, ,∴
,∴ ,∴
,∴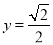 ,
,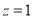 ,
,
∴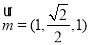 , 7分
, 7分
由(1)可得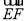 为平面
为平面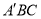 的法向量,且
的法向量,且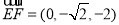 , 9分
, 9分
∴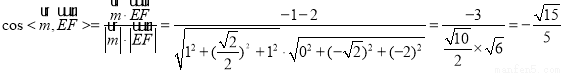 , 11分
, 11分
又∵二面角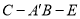 为锐二面角,∴二面角
为锐二面角,∴二面角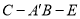 的余弦值为
的余弦值为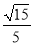 . 12分
. 12分
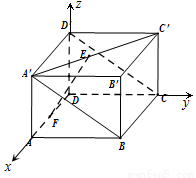
考点:1.线面垂直的性质;2.空间向量的运用.


科目:高中数学 来源:2014-2015学年湖北省黄冈市高三上学期元月调研考试文科数学试卷(解析版) 题型:解答题
已知数列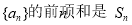 ,且
,且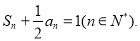
(Ⅰ)求数列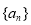 的通项公式;
的通项公式;
(Ⅱ)设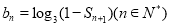 ,求适合方程
,求适合方程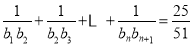 的正整数
的正整数 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省九江市第一次高考模拟统一考试文科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4—4:坐标系与参数方程
已知直线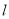 的参数方程为
的参数方程为 (
(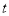 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,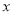 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线 的极坐标方程是
的极坐标方程是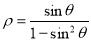 .
.
(1)写出直线 的极坐标方程与曲线
的极坐标方程与曲线 的普通方程;
的普通方程;
(2)若点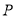 是曲线
是曲线 上的动点,求
上的动点,求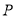 到直线
到直线 距离的最小值,并求出此时
距离的最小值,并求出此时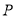 点的坐标.
点的坐标.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省九江市第一次高考模拟统一考试理科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4—4:坐标系与参数方程
已知直线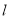 的参数方程为
的参数方程为 (
(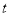 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,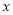 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线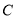 的极坐标方程是
的极坐标方程是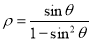 .
.
(1)写出直线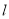 的极坐标方程与曲线
的极坐标方程与曲线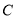 的普通方程;
的普通方程;
(2)若点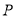 是曲线
是曲线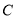 上的动点,求
上的动点,求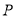 到直线
到直线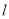 距离的最小值,并求出此时
距离的最小值,并求出此时 点的坐标.
点的坐标.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省九江市第一次高考模拟统一考试理科数学试卷(解析版) 题型:选择题
在如下程序框图中,输入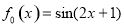 ,若输出的
,若输出的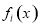 是
是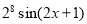 ,则程序框图中的判断框应填入( )
,则程序框图中的判断框应填入( )
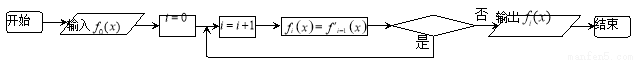
A.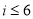 B.
B. C.
C.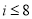 D.
D.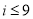
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省长望浏宁四县高三3月调研(一模)考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分)
某网站针对“2015年春节放假安排”开展网上问卷调查,提出了A,B两种放假方案,调查结果如下表(单位:万人):
人群 | 青少年 | 中年人 | 老年人 |
支持A方案 | 200 | 400 | 800 |
支持B方案 | 100 | 100 |
|
已知从所有参与调查的人中任选1人是“老年人”的概率为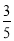 .
.
(Ⅰ)求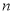 的值;
的值;
(Ⅱ)从参与调查的“老年人”中,用分层抽样的方法抽取6人,在这6人中任意选取2人,求恰好有1人“支持B方案”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com