Question

10．某锥体的三视图如图所示，则该几何体的体积为$\frac{8}{3}$，表面积为$6+2\sqrt{3}+4\sqrt{2}$．

Answer 1

分析 通过由三视图可知该椎体位于边长为2的正方体ABCD-EFGH的内部，利用体积公式及表面积公式计算即可．

解答 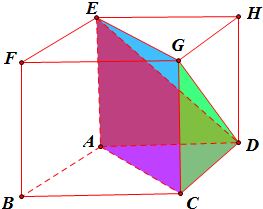解：由三视图可知，该椎体为三棱锥D-ACGE，
由三视图中的数据可知正方体ABCD-EFGH的边长为2，
∴V_D-ACGE=$\frac{1}{3}$•AC•AE•$\frac{1}{2}$BD=$\frac{1}{3}•$2$\sqrt{2}$•2•$\frac{2\sqrt{2}}{2}$=$\frac{8}{3}$，
S_D-ACGE=S_矩形ACGE+S_△ACD+S_△CDG+S_△DEG+S_△ADE
=$2•2\sqrt{2}$+$\frac{1}{2}•2•2$+$\frac{1}{2}•2•2$+$\frac{1}{2}•$$\sqrt{{2}^{2}+（\frac{2\sqrt{2}}{2}）^{2}}$•2$\sqrt{2}$+$\frac{1}{2}•2•2$
=6+2$\sqrt{3}$+4$\sqrt{2}$，
故答案为：$\frac{8}{3}$，6+2$\sqrt{3}$+4$\sqrt{2}$．

点评 本题以正方体为载体，考查利用三视图求空间几何体的体积和表面积，考查空间想象能力和逻辑思维能力，注意解题方法的积累，属于中档题．