
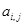 ,且满足
,且满足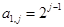 ,
,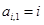 ,
,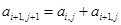 (
(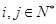 );又记第3行的数3,5,8,13,22,39……为数列{bn},则
);又记第3行的数3,5,8,13,22,39……为数列{bn},则
科目:高中数学 来源:不详 题型:解答题
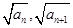 )在双曲线y2-x2=1上,点(
)在双曲线y2-x2=1上,点(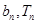 )在直线y=-
)在直线y=-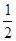 x+1上,其中Tn是数列{bn}的前n项和。
x+1上,其中Tn是数列{bn}的前n项和。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为正整数
,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为正整数 ,公比为正整数
,公比为正整数 的无穷等比数列
的无穷等比数列 的子数列问题. 为此,他任取了其中三项
的子数列问题. 为此,他任取了其中三项 .
. 成等比数列,求
成等比数列,求 之间满足的等量关系;
之间满足的等量关系; 中存在一个子数列
中存在一个子数列 是等差数列”,为此,他研究了
是等差数列”,为此,他研究了 与
与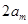 的大小关系,请你根据该同学的研究结果来判断上述猜想是否正确;
的大小关系,请你根据该同学的研究结果来判断上述猜想是否正确; ,公差为正整数
,公差为正整数 的无穷等差数列中是否存在成等比数列的子数列?请你就此问题写出一个正确命题,并加以证明.
的无穷等差数列中是否存在成等比数列的子数列?请你就此问题写出一个正确命题,并加以证明.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
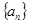 的前
的前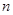 项和记为
项和记为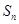 ,且满足
,且满足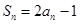 .
.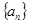 的通项公式;
的通项公式;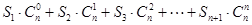 ;
;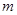 项的数列
项的数列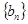 是连续的正整数数列,并且满足:
是连续的正整数数列,并且满足: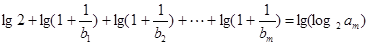 .
.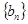 最多有几项?并求这些项的和.
最多有几项?并求这些项的和.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 个几何体的表面积是__________个平方单位.
个几何体的表面积是__________个平方单位. 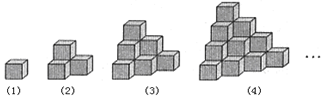
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com