
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源:不详 题型:解答题
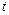 元(其中
元(其中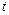 为常数,且
为常数,且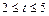 ),设该工厂每件玩具的出厂价为
),设该工厂每件玩具的出厂价为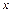 元(
元(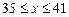 ),根据市场调查,日销售量与
),根据市场调查,日销售量与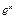 (
(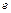 为自然对数的底数)成反比例,当每件玩具的出厂价为40元时,日销售量为10件.
为自然对数的底数)成反比例,当每件玩具的出厂价为40元时,日销售量为10件.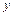 (元)与每件玩具的出厂价
(元)与每件玩具的出厂价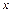 元的函数关系式;
元的函数关系式;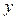 最大,并求
最大,并求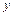 的最大值.
的最大值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
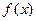 是定义在
是定义在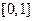 上的函数,若存在
上的函数,若存在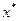
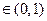 ,使得
,使得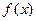 在
在 上单调递增,在
上单调递增,在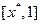 上单调递减,则称
上单调递减,则称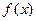 为
为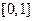 上的单峰函数,
上的单峰函数,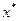 为峰点,包含峰点的区间为含峰区间. 对任意的
为峰点,包含峰点的区间为含峰区间. 对任意的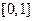 上的单峰函数
上的单峰函数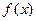 ,下面研究缩短其含峰区间长度的方法.
,下面研究缩短其含峰区间长度的方法.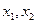
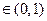 ,
, ,若
,若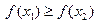 ,则
,则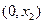 为含峰区间;若
为含峰区间;若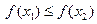 ,则
,则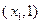 为含峰区间;
为含峰区间; ,证明:存在
,证明:存在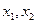
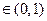 ,满足
,满足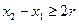 ,使得由(1)所确定的含峰区间的长度不大于
,使得由(1)所确定的含峰区间的长度不大于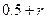 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 上规划出一块长方形地面建造公园,公园一边落在CD上,但不得越过文物保护区
上规划出一块长方形地面建造公园,公园一边落在CD上,但不得越过文物保护区 的EF.问如何设计才能使公园占地面积最大,并求这最大面积.( 其中AB=200m,BC=160m,AE=60m,AF=40m.)
的EF.问如何设计才能使公园占地面积最大,并求这最大面积.( 其中AB=200m,BC=160m,AE=60m,AF=40m.)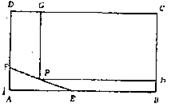
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.不会提高70% | B.会高于70%,但不会高于90% |
| C.不会低于10% | D.高于30%,但低于100% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com