
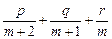 =0,其中m>0,求证:
=0,其中m>0,求证: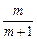 )<0;
)<0; 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源:不详 题型:单选题
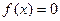 在[0,1]内的近似解,用“二分法”计算到
在[0,1]内的近似解,用“二分法”计算到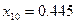 达到精确度要求。那么所取误差限
达到精确度要求。那么所取误差限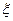 是( )
是( )| A.0.05 | B.0.005 | C.0.0005 | D.0.00005 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
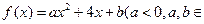 R),设关于
R),设关于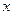 的方程
的方程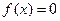 的两实根为
的两实根为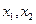 ,方程
,方程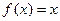 的两实根为
的两实根为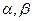 .(Ⅰ)若
.(Ⅰ)若 ,求
,求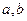 的关系式;(Ⅱ)若
的关系式;(Ⅱ)若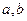 均为负整数,且
均为负整数,且 ,求
,求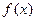 的解析式; (Ⅲ)若
的解析式; (Ⅲ)若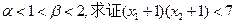 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 唯一的一个零点同时在区间
唯一的一个零点同时在区间 、
、 、
、 、
、 内,
内,A.函数 在区间 在区间 内有零点 内有零点 |
B.函数 在区间 在区间 或 或 内有零点 内有零点 |
C.函数 在区间 在区间 内无零点 内无零点 |
D.函数 在区间 在区间 内无零点 内无零点 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com