练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

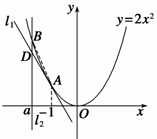
    如图所示，已知A(－1,2)为抛物线C：y＝2x2上的点，直线l1过点A，且与抛物线C相切，直线l2：x＝a (a<－1)交抛物线C于点B，交直线l1于点D.

    (1)求直线l1的方程；

    (2)求△ABD的面积S1.


    解　(1)由条件知点A(－1,2)为直线l1与抛物线C的切点，

    ∵y′＝4x，∴直线l1的斜率k＝－4，

    所以直线l1的方程为y－2＝－4(x＋1)，

    即4x＋y＋2＝0.

    (2)点A的坐标为(－1,2)，

    由条件可求得点B的坐标为(a,2a2)，

    点D的坐标为(a，－4a－2)，∴△ABD的面积为

    S1＝×|2a2－(－4a－2)|×|－1－a|

    ＝|(a＋1)3|＝－(a＋1)3.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


     “x＝”是“函数y＝sin 2x取得最大值”的____________条件．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    直线y＝a与函数f(x)＝x3－3x的图象有相异的三个公共点，则a的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝x3－3ax－1，a≠0.

    (1)求f(x)的单调区间；

    (2)若f(x)在x＝－1处取得极值，直线y＝m与y＝f(x)的图象有三个不同的交点，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若曲线f(x)=x4-x在点P处的切线平行于直线3x-y=0,则点P的坐标为          .

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某种电热水器的水箱盛满水是200升，加热到一定温度可浴用，浴用时，已知每分钟放

    水34升，在放水的同时注水，t分钟注入2t2升，当水箱内水量达到最小值时，放水自动停止，现假定每人洗浴用水65升，则该热水器一次至多可供________人洗浴．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某地上年度电价为0.8元，年用电量为1亿千瓦时．本年度计划将电价调至0.55

    元～0.75元之间，经测算，若电价调至x元，则本年度新增用电量y(亿千瓦时)与(x－0.4)元成反比例．又当x＝0.65时，y＝0.8.

    (1)求y与x之间的函数关系式；

    (2)若每千瓦时电的成本价为0.3元，则电价调至多少时，本年度电力部门的收益将比上年增加20%？[收益＝用电量×(实际电价－成本价)]

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知集合M＝{x|0<x<1}，集合N＝{x|－2<x<1}，那么“a∈N”是“a∈M”的

    ______________条件．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)＝3ax－2a＋1在区间[－1,1]上存在一个零点，则a的取值范围是______________．

    查看答案和解析>>

    同步练习册答案