
分析 (1)由题意可以分为两类,分别求出每一类的概率,再根据概率的公式计算即可;
(2)求出2名同学同时来同一个班的概率,再根据互斥事件的概率公式计算即可.
解答 解:(1)甲选男且乙选女的概率为P1=$\frac{1}{3}$×$\frac{1}{2}$=$\frac{1}{6}$,
甲选女且乙选男的概率为P2=$\frac{2}{3}$×$\frac{1}{2}$=$\frac{1}{3}$,
故2名同学是异性同学的概率P=$\frac{1}{6}$+$\frac{1}{3}$=$\frac{1}{2}$,
(2)从报名的5名同学中任选2名同学共有10种方法,
2名同学全来自甲班的选法由C32=3种,
2名同学全来自乙班的选法由C22=1种,
故同时来同一个班的概率P=$\frac{3+1}{10}$=$\frac{2}{5}$,
故这2名同学不能同时来同一个班的概率P=1-$\frac{2}{5}$=$\frac{3}{5}$
点评 本题考查了概率的基本性质,掌握基本的概率公式,属于基础题.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 金额分组 | [1,5) | [5,9) | [9,13) | [13,17) | [17,21) | [21,25) |
| 频数 | 3 | 9 | 17 | 11 | 8 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
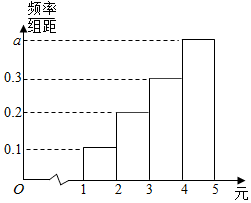 甲、乙、丙三人参加微信群抢红包游戏,规则如下:每轮游戏发10个红包,每个红包金额在[1,5]产生.已知在每轮游戏中所产生的10个红包金额的频率分布直方图如图所示.
甲、乙、丙三人参加微信群抢红包游戏,规则如下:每轮游戏发10个红包,每个红包金额在[1,5]产生.已知在每轮游戏中所产生的10个红包金额的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在五面体ABCDE中,AD⊥平面ABC,AD∥BE∥CF,△ABC为等边三角形,AB=2$\sqrt{3}$,BE=2,AD=3,CF=4,M为EF的中点.
如图,在五面体ABCDE中,AD⊥平面ABC,AD∥BE∥CF,△ABC为等边三角形,AB=2$\sqrt{3}$,BE=2,AD=3,CF=4,M为EF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com