
定义方程f(x)=f ′(x)的实数根x0叫做函数f(x)的“新驻点”,若函数g(x)=x,h(x)=ln(x+1),φ(x)=x3-1的“新驻点”分别为α、β、γ,则α、β、γ的大小关系为( )
A.α>β>γ B.β>α>γ
C.γ>α>β D.β>γ>α
科目:高中数学 来源: 题型:
一个蜂巢里有1只蜜蜂,第一天,它飞出去带回了5个伙伴;第二天,6只蜜蜂飞出去各自带回了5个伙伴……如果这个过程继续下去,那么第6天所有蜜蜂归巢后,蜂巢中共有蜜蜂( )
A. 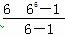 只 B.66只
只 B.66只
C.63只 D.62只
查看答案和解析>>
科目:高中数学 来源: 题型:
等比数列{an}中,a1=2,a8=4,f(x)=x(x-a1)(x-a2)…(x-a8),f ′(x)为函数f(x)的导函数,则f ′(0)=( )
A.0 B.26
C.29 D.212
查看答案和解析>>
科目:高中数学 来源: 题型:
已知e为自然对数的底数,设函数f(x)=(ex-1)(x-1)k(k=1,2),则( )
A.当k=1时,f(x)在x=1处取到极小值
B.当k=1时,f(x)在x=1处取到极大值
C.当k=2时,f(x)在x=1处取到极小值
D.当k=2时,f(x)在x=1处取到极大值
查看答案和解析>>
科目:高中数学 来源: 题型:
某食品厂进行蘑菇的深加工,每公斤蘑菇的成本20元,并且每公斤蘑菇的加工费为t元(t为常数,且2≤t≤5),设该食品厂每公斤蘑菇的出厂价为x元(25≤x≤40),根据市场调查,日销售量q与ex成反比,当每公斤蘑菇的出厂价为30元时,销售量为100kg.(每日利润=日销售量×(每公斤出厂价-成本价-加工费)).
(1)求该工厂的每日利润y元与每公斤蘑菇的出厂价x元的函数关系式;
(2)若t=5,当每公斤蘑菇的出厂价x为多少元时,该工厂的利润y最大,并求最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com