
分析 用$\overrightarrow{AB}$,$\overrightarrow{AD}$表示出$\overrightarrow{AM}$,$\overrightarrow{NM}$,在进行计算.
解答 解:∵$\overrightarrow{BM}$=3$\overrightarrow{MC}$,$\overrightarrow{DN}$=2$\overrightarrow{NC}$,
∴$\overrightarrow{NC}=\frac{1}{3}\overrightarrow{DC}=\frac{1}{3}\overrightarrow{AB}$,$\overrightarrow{CM}=-\frac{1}{4}\overrightarrow{BC}=-\frac{1}{4}\overrightarrow{AD}$,$\overrightarrow{BM}$=$\frac{3}{4}\overrightarrow{BC}$=$\frac{3}{4}\overrightarrow{AD}$.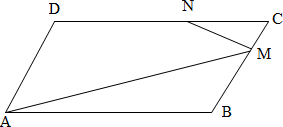
∴$\overrightarrow{AM}$=$\overrightarrow{AB}+\overrightarrow{BM}$=$\overrightarrow{AB}+\frac{3}{4}\overrightarrow{AD}$,$\overrightarrow{NM}$=$\overrightarrow{NC}+\overrightarrow{CM}$=$\frac{1}{3}\overrightarrow{AB}$-$\frac{1}{4}$$\overrightarrow{AD}$.
∴$\overrightarrow{AM}$$•\overrightarrow{NM}$=($\overrightarrow{AB}+\frac{3}{4}\overrightarrow{AD}$)•($\frac{1}{3}\overrightarrow{AB}$-$\frac{1}{4}$$\overrightarrow{AD}$)=$\frac{1}{3}{\overrightarrow{AB}}^{2}$-$\frac{3}{16}{\overrightarrow{AD}}^{2}$=$\frac{1}{3}×$36-$\frac{3}{16}×16$=9.
故答案为:9.
点评 本题考查了平面向量的数量积运算,属于中档题.


科目:高中数学 来源: 题型:解答题
 水是最常见的物质之一,是包括人类在内所有生命生存的重要资源,也是生物体最重要的组成部分.为了推动对水资源进行综合性统筹规划和管理,加强水资源保护,解决日益严峻的淡水缺乏问题,开展广泛的宣传以提高公众对开发和保护水资源的认识.中国水利部确定每年的3月22日至28日为“中国水周”,以提倡市民节约用水.某市统计局调查了该市众多家庭的用水量情况,绘制了月用水量的频率分布直方图,如图所示.将月用水量落入各组的频率视为概率,并假设每天的用水量相互独立.
水是最常见的物质之一,是包括人类在内所有生命生存的重要资源,也是生物体最重要的组成部分.为了推动对水资源进行综合性统筹规划和管理,加强水资源保护,解决日益严峻的淡水缺乏问题,开展广泛的宣传以提高公众对开发和保护水资源的认识.中国水利部确定每年的3月22日至28日为“中国水周”,以提倡市民节约用水.某市统计局调查了该市众多家庭的用水量情况,绘制了月用水量的频率分布直方图,如图所示.将月用水量落入各组的频率视为概率,并假设每天的用水量相互独立.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1009 | B. | 1010 | C. | 1009,1010 | D. | 2016 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,扇形OAB的中心角为直角,半径为1,点P为扇形OAB的弧$\widehat{AB}$上任意一点,设$\overrightarrow{OP}$=x$\overrightarrow{OB}$+y$\overrightarrow{OA}$(x,y∈R),$\overrightarrow a$=(x,y),$\overrightarrow b$=(${\sqrt{3}$,1),则$\overrightarrow a•\overrightarrow b$的最小值为( )
如图,扇形OAB的中心角为直角,半径为1,点P为扇形OAB的弧$\widehat{AB}$上任意一点,设$\overrightarrow{OP}$=x$\overrightarrow{OB}$+y$\overrightarrow{OA}$(x,y∈R),$\overrightarrow a$=(x,y),$\overrightarrow b$=(${\sqrt{3}$,1),则$\overrightarrow a•\overrightarrow b$的最小值为( )| A. | -1 | B. | -2 | C. | 1 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+$\sqrt{5}$ | B. | $\frac{10}{3}$ | C. | 2$\sqrt{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
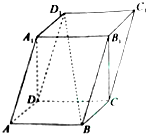 已知四棱柱ABCD-A1B1C1D1,侧面A1ADD1⊥面ABCD,底面ABCD是矩形,且AB=2,AD=1,AA1=$\sqrt{5}$,∠A1AD的余弦值为$\frac{\sqrt{5}}{5}$.
已知四棱柱ABCD-A1B1C1D1,侧面A1ADD1⊥面ABCD,底面ABCD是矩形,且AB=2,AD=1,AA1=$\sqrt{5}$,∠A1AD的余弦值为$\frac{\sqrt{5}}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 售价(单位:元) | 23 | 21 | 20 |
| 日销量(单位:个) | 10 | 15 | 20 |
| 频数 | 4 | 14 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com