
分析 根据二项式${(\frac{1}{2}\sqrt{x}+\frac{2}{\root{3}{x}})}^{6}$展开式的通项公式,求出第四项的系数即可.
解答 解:二项式${(\frac{1}{2}\sqrt{x}+\frac{2}{\root{3}{x}})}^{6}$展开式中,
第四项为T3+1=${C}_{6}^{3}$•${(\frac{1}{2}\sqrt{x})}^{6-3}$•${(\frac{2}{\root{3}{x}})}^{3}$,
∴展开式中第四项的系数为:
${C}_{6}^{3}$•${(\frac{1}{2})}^{3}$•23=20.
故答案为:20.
点评 本题考查了二项式展开式的通项公式应用问题,是基础题目.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
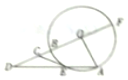 如图,圆O的半径OA与OB相互垂直,E为圆O上一点,直线OB与圆O交于另一点F,与直线AE交于点D,过点E的切线CE交线段于点C,求证:CD2=CB•CF.
如图,圆O的半径OA与OB相互垂直,E为圆O上一点,直线OB与圆O交于另一点F,与直线AE交于点D,过点E的切线CE交线段于点C,求证:CD2=CB•CF.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 线性正相关关系 | |
| B. | 由回归方程无法判断其正负相关关系 | |
| C. | 线性负相关关系 | |
| D. | 不存在线性相关关系 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∨(¬q) | C. | p∧(¬q) | D. | (¬p)∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1190秒 | B. | 1195秒 | C. | 1200秒 | D. | 1205秒 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com