Question

一个多面体的三视图如图所示，M，N分别是A₁B、B₁C₁点中点．
（Ⅰ）求证：MN⊥平面A₁BC；
（Ⅱ）求直线BC₁与平面A₁BC所成角的大小；
（Ⅲ）求二面角A-A₁B-C的大小．

Answer 1

考点：二面角的平面角及求法,直线与平面垂直的判定,直线与平面所成的角

专题：空间位置关系与距离,空间角

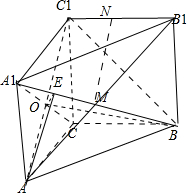
分析：（Ⅰ）连接AC₁，AB₁，便能得到MN∥AC₁，并且容易证明AC₁⊥平面A₁BC，这样即可得到MN⊥平面A₁BC．
（Ⅱ）通（Ⅰ）容易得到∠OBC₁为直线BC₁和平面A₁BC所成的角，在Rt△OBC₁中，根据边的关系求出这个角即可．
（Ⅲ）先作出二面角的平面角，根据（Ⅰ）过O作OE⊥A₁B，交A₁B于E，连接AE，容易得出∠AEO即为所求二面角的平面角，在Rt△AOE中根据变的关系求出即可．

解答： 解：（Ⅰ）连接AC₁，AB₁，则MN∥AC₁，BC⊥平面ACC₁A₁，AC₁?平面ACC₁A₁；
∴BC⊥AC₁，即AC₁⊥BC，又AC₁⊥A₁C，A₁C∩BC=C；
∴AC₁⊥平面A₁BC，∴MN⊥平面A₁BC．
（Ⅱ）设AC₁∩A₁C=O，连接OB，则：∠C₁BO即为直线BC₁与平面A₁BC所成角，在Rt△C₁BO中：
C1O=

2

2

a，BC1=

2

a，∠C1OB=90°；
∴sin∠C1BO=

1

2

，∴∠C₁BO=30°；
∴直线BC₁与平面A₁BC所成角为30°．
（Ⅲ）过O作OE⊥A₁B，交A₁B于E，连接AE；
∵AC₁⊥平面A₁BC，∴A₁B⊥AE；
∴∠OEA即为二面角A-A₁B-C的平面角；
sin∠CA1B=

a

3 a

=

3

3

，∴OE=

2 a

2

•

3

3

=

6 a

6

；
∴在Rt△AOE中，tan∠OEA=

2 a 2

6 a 6

=

3

，∴∠OEA=60°；
∴二面角A-A₁B-C的大小为60°．∬

点评：考查线面垂直的判定定理，线面角的概念及求法，直角三角形边角的关系，二面角的概念、二面角的平面角的概念及求法．