考点:利用导数研究函数的极值,利用导数求闭区间上函数的最值
专题:综合题,导数的综合应用
分析:(1)由f(x)=e
x-ax+a,知f′(x)=e
x-a,再由a的符号进行分类讨论,能求出f(x)的单调区间,然后根据交点求出a的取值范围;
(2)由x
1、x
2的关系,求出
f′()<0,然后再根据f′(x)=e
x-a的单调性,利用不等式的性质,问题得以证明;
(3)F(x)是偶函数,可得f(x)+e
-x≥g(x)对x∈R恒成立?F(x)≥0对x∈[0,+∞)恒成立.分类讨论,确定函数的单调性,即可求a取值范围.
解答:
(1)解:f'(x)=e
x-a.
若a≤0,则f'(x)>0,则函数f(x)是单调增函数,这与题设矛盾.
∴a>0,令f'(x)=0,则x=lna.
当x<lna时,f'(x)<0,f(x)是单调减函数;x>lna时,f'(x)>0,f(x)是单调增函数;
于是当x=lna时,f(x)取得极小值.
∵函数f(x)=e
x-ax+a(a∈R)的图象与x轴交于两点A(x
1,0),B(x
2,0)(x
1<x
2),
∴f(lna)=a(2-lna)<0,
即a>e
2.此时,存在1<lna,f(1)=e>0;
存在3lna>lna,f(3lna)=a
3-3alna+a>a
3-3a
2+a>0,
又f(x)在R上连续,故a>e
2为所求取值范围.…(4分)
(2)证明:∵
两式相减得
a=.
记
=s(s>0),则
f′()=e-=[2s-(es-e-s)],
设g(s)=2s-(e
s-e
-s),则g′(s)=2-(e
s+e
-s)<0,∴g(s)是单调减函数,
则有g(s)<g(0)=0,而
>0,∴
f′()<0.
又f'(x)=e
x-a是单调增函数,且
>∴
f′()<0. …(8分)
(3)解:设F(x)=f(x)+e
-x-g(x)=e
x+e
-x-3ax
2-2
∵F(-x)=F(x),
∴F(x)是偶函数
∴f(x)+e
-x≥g(x)对x∈R恒成立?F(x)≥0对x∈[0,+∞)恒成立.
F′(x)=e
x-e
-x-6ax,设h(x)=(F′(x))′=e
x+e
-x-6a
∴h′(x)=e
x+e
-x=
≥0
∴h(x)在x∈[0,+∞)上单调递增,h(x)≥h(0)=2-6a
①当
2-6a≥0?a≤时,h(x)≥h(0)=2-6a≥0⇒F′(x)在x∈[0,+∞)上单调递增
∴F′(x)≥F′(0)=0,
∴F(x)在x∈[0,+∞)上单调递增
∴F(x)≥F(0)=0对x∈[0,+∞)恒成立
②当
2-6a<0?a>时,h(0)=2-6a<0
∵h(x)在x∈[0,+∞)上单调递增,又
h(ln6a)=>0故?x
0∈(0,+∞),使h(x
0)=0
当x∈(0,x
0)时,h(x)<0⇒F′(x)在(0,x
0)单调递减⇒F′(x)<F′(x)=0
当x∈(0,x
0)时,F(x)单调递减,此时,F(x)≥F(0)=0对x∈[0,+∞)不恒成立
综上,当
a≤时,F(x)≥0对x∈[0,+∞)恒成立,即f(x)+e
-x≥g(x)对x∈R恒成立 …(14分)
点评:本题属于难题,考查分类讨论的思想,转化思想,方程思想,做题要认真仔细,方法要明,过程要严谨,能提高分析问题解决问题的能力.



 孟建平名校考卷系列答案
孟建平名校考卷系列答案 如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=
如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=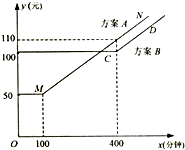 移动公司根据市场客户的不同需求,对某地区的手机套餐通话费提出两种优惠方案,两种方案所付电话费(元)与通话时间(分钟)之间的关系如图所示(实线部分:MN与CD平行即直线方程y=kx+b中的斜率k相等).
移动公司根据市场客户的不同需求,对某地区的手机套餐通话费提出两种优惠方案,两种方案所付电话费(元)与通话时间(分钟)之间的关系如图所示(实线部分:MN与CD平行即直线方程y=kx+b中的斜率k相等).