
| A. | $\frac{1}{2}$ | B. | 1-$\frac{\sqrt{2}}{3}$ | C. | $\frac{3}{4}$ | D. | 1+$\frac{\sqrt{3}}{2}$ |
分析 设|AB|=c,|AC|=b,进行数量积运算便可得到 $\overrightarrow{AP}$•$\overrightarrow{AB}$=$\frac{1}{2}$c2,$\overrightarrow{AP}$•$\overrightarrow{AC}$=$\frac{1}{2}$b2;根据条件在$\overrightarrow{AP}$=λ1$\overrightarrow{AB}$+2λ2$\overrightarrow{AC}$两边分别乘以$\overrightarrow{AB}$,$\overrightarrow{AC}$,进行数量积运算,并整理可得到$\left\{\begin{array}{l}\frac{1}{2}{c}^{\;}={λ}_{1}{c}^{\;}+{λ}_{2}b\\ \frac{1}{2}{b}^{\;}=\frac{1}{2}{λ}_{1}{c}^{\;}+2{λ}_{2}{b}^{\;}\end{array}\right.$,
消元即可得出$\left\{\begin{array}{l}{λ}_{1}{=\frac{2}{3}}^{\;}-\frac{1}{3}•\frac{b}{c}\\{λ}_{2}{{=\frac{1}{3}}^{\;}-\frac{1}{6}•\frac{c}{b}}^{\;}\end{array}\right.$,从而表示出λ1+λ2,根据基本不等式即可求出λ1+λ2的最大值.,从而表示出x+y,根据基本不等式即可求出x+y的最大值
解答 解:设|AB|=c,|AC|=b,
则:$\overrightarrow{AP}$•$\overrightarrow{AB}$=$\frac{1}{2}$c2,$\overrightarrow{AP}$•$\overrightarrow{AC}$=$\frac{1}{2}$b2;
又cosA=$\frac{1}{2}$,在$\overrightarrow{AP}$=λ1$\overrightarrow{AB}$+2λ2$\overrightarrow{AC}$的两边分别乘以$\overrightarrow{AB}$,$\overrightarrow{AC}$得:$\left\{\begin{array}{l}\frac{1}{2}{c}^{2}={λ}_{1}{c}^{2}+{λ}_{2}bc\\ \frac{1}{2}{b}^{2}=\frac{1}{2}{λ}_{1}{bc}^{\;}+2{λ}_{2}{b}^{2}\end{array}\right.$;
整理得,$\left\{\begin{array}{l}\frac{1}{2}{c}^{\;}={λ}_{1}{c}^{\;}+{λ}_{2}b\\ \frac{1}{2}{b}^{\;}=\frac{1}{2}{λ}_{1}{c}^{\;}+2{λ}_{2}{b}^{\;}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{λ}_{1}{=\frac{2}{3}}^{\;}-\frac{1}{3}•\frac{b}{c}\\{λ}_{2}{{=\frac{1}{3}}^{\;}-\frac{1}{6}•\frac{c}{b}}^{\;}\end{array}\right.$;
∴λ1+λ2=1-($\frac{b}{3c}$+$\frac{c}{6b}$)≤1-2$\sqrt{\frac{1}{18}}$=1-$\frac{\sqrt{2}}{3}$;
∴λ1+λ2的最大值为 1-$\frac{\sqrt{2}}{3}$.
故选:B
点评 考查向量数量积的运算及计算公式,三角形的外心的概念,消元法解二元一次方程组,以及基本不等式求最值,不等式的性质.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{19}{41}$ | B. | $\frac{17}{37}$ | C. | $\frac{7}{15}$ | D. | $\frac{20}{41}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[2\sqrt{2}-3,\frac{56}{9}]$ | B. | $[\frac{56}{9},+∞)$ | C. | $(-∞,2\sqrt{2}-3]$ | D. | $(-∞,2\sqrt{2}-3]∪[\frac{56}{9},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $a=1,b=\sqrt{2},A={30°}$ | B. | $b=\sqrt{2},c=2,B={45°}$ | C. | a=1,b=2,c=3 | D. | a=3,b=2,A=60° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
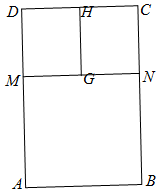 拟用长度为l的钢筋焊接一个如图所示的矩形框架结构(钢筋体积、焊接点均忽略不计),其中G、H分别为框架梁MN、CD的中点,MN∥CD,设框架总面积为S平方米,BN=2CN=2x米.
拟用长度为l的钢筋焊接一个如图所示的矩形框架结构(钢筋体积、焊接点均忽略不计),其中G、H分别为框架梁MN、CD的中点,MN∥CD,设框架总面积为S平方米,BN=2CN=2x米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com