
| A. | $\frac{19}{41}$ | B. | $\frac{17}{37}$ | C. | $\frac{7}{15}$ | D. | $\frac{20}{41}$ |
分析 利用等差数列的通项公式性质可得:$\frac{{{a_3}+{a_{15}}}}{{2({{b_3}+{b_9}})}}$=$\frac{2{a}_{9}}{2({b}_{3}+{b}_{9})}$,可得$\frac{{{a_3}+{a_{15}}}}{{2({{b_3}+{b_9}})}}$+$\frac{a_3}{{{b_2}+{b_{10}}}}$=$\frac{{a}_{9}}{{b}_{1}+{b}_{11}}$+$\frac{{a}_{3}}{{b}_{1}+{b}_{11}}$,再进行转化利用求和公式及其性质即可得出.
解答 解:∵等差数列中,若m+n=p+q,则am+an=ap+aq;
等差数列的前n项和为:Sn=$\frac{({a}_{1}+{a}_{n})n}{2}$.
∴$\frac{{{a_3}+{a_{15}}}}{{2({{b_3}+{b_9}})}}$=$\frac{2{a}_{9}}{2({b}_{3}+{b}_{9})}$=$\frac{{a}_{9}}{{b}_{3}+{b}_{9}}$
∴$\frac{{{a_3}+{a_{15}}}}{{2({{b_3}+{b_9}})}}$+$\frac{a_3}{{{b_2}+{b_{10}}}}$
=$\frac{{a}_{9}}{{b}_{3}+{b}_{9}}$+$\frac{{a}_{3}}{{b}_{2}+{b}_{10}}$=$\frac{{a}_{9}}{{b}_{1}+{b}_{11}}$+$\frac{{a}_{3}}{{b}_{1}+{b}_{11}}$
=$\frac{{a}_{3}+{a}_{9}}{{b}_{1}+{b}_{11}}$=$\frac{{a}_{1}+{a}_{11}}{{b}_{1}+{b}_{11}}$=$\frac{\frac{11({a}_{1}+{a}_{11})}{2}}{\frac{11({b}_{1}+{b}_{11})}{2}}$
=$\frac{{S}_{11}}{{T}_{11}}$=$\frac{2×11-3}{4×11-3}$
=$\frac{19}{41}$
故选:A.
点评 本题考查等差数列的通项公式及其性质及其求和公式,考查了推理能力与计算能力,属于中档题.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[-1,\frac{1}{3})$ | B. | $[0,\frac{1}{3}]$ | C. | [3,+∞) | D. | (-1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
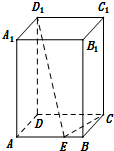 如图,在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=$\sqrt{3}$,点E为棱AB上的动点,则D1E+CE的最小值为( )
如图,在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=$\sqrt{3}$,点E为棱AB上的动点,则D1E+CE的最小值为( )| A. | $2\sqrt{2}$ | B. | $\sqrt{10}$ | C. | $2+\sqrt{2}$ | D. | $\sqrt{5}+1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1-$\frac{\sqrt{2}}{3}$ | C. | $\frac{3}{4}$ | D. | 1+$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com