
分析 $f(x)=\frac{1}{{1+{2^x}}}$对称中心为$(0,\frac{1}{2})$,由此能求出结果.
解答 解:∵$f(x)+f(0-x)=\frac{1}{{1+{2^x}}}+\frac{1}{{1+{2^{-x}}}}=1$,
∴$f(x)=\frac{1}{{1+{2^x}}}$对称中心为$(0,\frac{1}{2})$,
∴$f(-\frac{1}{3})+f(-1)+f(0)+f(1)+f(\frac{1}{3})=5f(0)=\frac{5}{2}$.
故答案为:$\frac{5}{2}$.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{19}{41}$ | B. | $\frac{17}{37}$ | C. | $\frac{7}{15}$ | D. | $\frac{20}{41}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
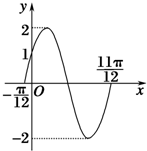 若f(x)=Asin(ωx+θ)(A>0,ω>0,|θ|<$\frac{π}{2}$)的图象如图所示,
若f(x)=Asin(ωx+θ)(A>0,ω>0,|θ|<$\frac{π}{2}$)的图象如图所示,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[2\sqrt{2}-3,\frac{56}{9}]$ | B. | $[\frac{56}{9},+∞)$ | C. | $(-∞,2\sqrt{2}-3]$ | D. | $(-∞,2\sqrt{2}-3]∪[\frac{56}{9},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com