
【题目】如图,在平面直角坐标系xOy中,椭圆C:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,短轴长是2.
,短轴长是2.
(1)求椭圆C的方程;
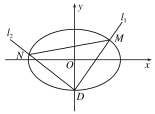
(2)设椭圆C的下顶点为D,过点D作两条互相垂直的直线l1,l2,这两条直线与椭圆C的另一个交点分别为M,N.设l1的斜率为k(k≠0),△DMN的面积为S,当![]() ,求k的取值范围.
,求k的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由e=![]() ,2b=2,a2=b2+c2构造方程组,解出a,b即可得椭圆方程;(2)设l1的方程为y=kx-1代入椭圆方程,求出M的坐标,可得|DM|,用
,2b=2,a2=b2+c2构造方程组,解出a,b即可得椭圆方程;(2)设l1的方程为y=kx-1代入椭圆方程,求出M的坐标,可得|DM|,用![]() 代替k,可得|DN|,求出△DMN的面积S,可得
代替k,可得|DN|,求出△DMN的面积S,可得![]() ,解不等式
,解不等式![]() >
>![]() 可得k的取值范围.
可得k的取值范围.
(1)设椭圆C的半焦距为c,则由题意得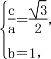 又a2=b2+c2,解得a=2,b=1,
又a2=b2+c2,解得a=2,b=1,
∴椭圆方程为![]() +y2=1.
+y2=1.
(2)由(1)知,椭圆C的方程为![]() +y2=1,
+y2=1,
所以椭圆C与y轴负半轴交点为D(0,-1).
因为l1的斜率存在,所以设l1的方程为y=kx-1.
代入![]() +y2=1,得M
+y2=1,得M![]() ,
,
从而|DM|=![]() =
=![]() .
.
用-![]() 代替k得|DN|=
代替k得|DN|=![]() .
.
所以△DMN的面积S=![]() ·
·![]() ×
×![]() =
=![]() .
.
则![]() =
=![]() ,
,
因为![]() >
>![]() ,即
,即![]() >
>![]() ,
,
整理得4k4-k2-14<0,解得-![]() <k2<2,
<k2<2,
所以0<k2<2,即-![]() <k<0或0<k<
<k<0或0<k<![]() .
.
从而k的取值范围为(-![]() ,0)∪(0,
,0)∪(0,![]() ).
).


科目:高中数学 来源: 题型:
【题目】如图,半径为![]() 的水轮绕着圆心
的水轮绕着圆心![]() 逆时针做匀速圆周运动,每分钟转动
逆时针做匀速圆周运动,每分钟转动![]() 圈,水轮圆心
圈,水轮圆心![]() 距离水面
距离水面![]() ,如果当水轮上点
,如果当水轮上点![]() 从离开水面的时刻(
从离开水面的时刻(![]() )开始计算时间.
)开始计算时间.
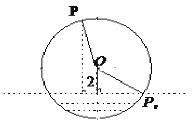
(1)试建立适当的平面直角坐标系,求点![]() 距离水面的高度
距离水面的高度![]() (
(![]() )与时间
)与时间![]() (
(![]() )满足的函数关系;
)满足的函数关系;
(2)求点![]() 第一次到达最高点需要的时间.
第一次到达最高点需要的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】旅行社为某旅行团包飞机去旅游,其中旅行社的包机费为![]() 元.旅行团中的每个人的飞机票按以下方式与旅行社结算:若旅行团的人数不超过
元.旅行团中的每个人的飞机票按以下方式与旅行社结算:若旅行团的人数不超过![]() 人时,飞机票每张
人时,飞机票每张![]() 元;若旅行团的人数多于
元;若旅行团的人数多于![]() 人时,则予以优惠,每多
人时,则予以优惠,每多![]() 人,每个人的机票费减少
人,每个人的机票费减少![]() 元,但旅行团的人数最多不超过
元,但旅行团的人数最多不超过![]() 人.设旅行团的人数为
人.设旅行团的人数为![]() 人,飞机票价格
人,飞机票价格![]() 元,旅行社的利润为
元,旅行社的利润为![]() 元.
元.
(1)写出每张飞机票价格![]() 元与旅行团人数
元与旅行团人数![]() 之间的函数关系式;
之间的函数关系式;
(2)当旅行团人数![]() 为多少时,旅行社可获得最大利润?求出最大利润.
为多少时,旅行社可获得最大利润?求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据.
x | 6 | 8 | 10 | 12 |
y | 2 | 3 | 5 | 6 |
(1)请根据上表提供的数据,求出y关于x的线性回归方程![]() ;
;
(2)判断该高三学生的记忆力x和判断力是正相关还是负相关;并预测判断力为4的同学的记忆力.
(参考公式: )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阿基米德(公元前287年—公元前212年),伟大的古希腊哲学家、数学家和物理学家,他死后的墓碑上刻着一个“圆柱容球”的立体几何图形,为纪念他发现“圆柱内切球的体积是圆柱体积的![]() ,且球的表面积也是圆柱表面积的
,且球的表面积也是圆柱表面积的![]() ”这一完美的结论.已知某圆柱的轴截面为正方形,其表面积为
”这一完美的结论.已知某圆柱的轴截面为正方形,其表面积为![]() ,则该圆柱的内切球体积为( )
,则该圆柱的内切球体积为( )
A.![]() B.
B.![]() C.
C.![]()
![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com