
【题目】已知函数![]() ,
,![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)设![]() ,当
,当![]() 时,判断是否存在
时,判断是否存在![]() 使得
使得![]() ,并证明你的结论.
,并证明你的结论.
【答案】(1)见解析(2)不存在;见解析
【解析】
(1)先对函数求导,得到![]() ,分别讨论
,分别讨论![]() ,
,![]() 两种情况,分别求解对应的不等式,即可得出结果;
两种情况,分别求解对应的不等式,即可得出结果;
(2)先由(1)得,![]() ,推出
,推出![]() ,由
,由![]() 时,
时,![]() ,得到
,得到![]() ,分别讨论
,分别讨论![]() ,
,![]() 两种情况,通过导数的方法研究函数的最值等,即可得出结果.
两种情况,通过导数的方法研究函数的最值等,即可得出结果.
(1)![]() 的定义域为
的定义域为![]() ,
,
由![]() ,得
,得![]() .
.
①若![]() ,则当
,则当![]() 时,
时,![]() ,
,
此时![]() 的单调递增区间为
的单调递增区间为![]() ,无单调递减区间;
,无单调递减区间;
②若![]() ,令
,令![]() ,解得
,解得![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
此时,![]() 的单调递增区间为
的单调递增区间为![]() ;单调递减区间为
;单调递减区间为![]() .
.
(2)当![]() 时,不存在
时,不存在![]() ,使得
,使得![]() ,证明如下:
,证明如下:
由(1)知,当![]() 时,
时,![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
所以![]() ,故
,故![]() ,即
,即![]() .
.
因为![]() ,所以当
,所以当![]() 时,
时,![]() ,故
,故![]() .
.
①当![]() 时,
时,![]() 再由
再由
令![]() ,则
,则![]() .
.
令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ;当
;当![]() ,
,![]() .
.
所以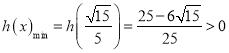 ,故
,故![]() ,
,
所以当![]() 时,对
时,对![]() ,都有
,都有![]() .
.
②当![]() 时,对于
时,对于![]() ,
,![]() ,故
,故![]() .
.
综合①,②,当![]() 时,对于任意的
时,对于任意的![]() ,都有
,都有![]() .
.
所以,当![]() 时,不存在
时,不存在![]() ,使得
,使得![]() .
.


科目:高中数学 来源: 题型:
【题目】“杂交水稻之父”袁隆平一生致力于杂交水稻技术的研究、应用与推广,发明了“三系法”籼型杂交水稻,成功研究出“两系法”杂交水稻,创建了超级杂交稻技术体系,为我国粮食安全、农业科学发展和世界粮食供给做出了杰出贡献;某杂交水稻种植研究所调查某地水稻的株高,得出株高(单位:cm)服从正态分布,其密度曲线函数为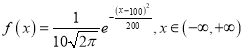 ,则下列说法正确的是( )
,则下列说法正确的是( )
A.该地水稻的平均株高为100cm
B.该地水稻株高的方差为10
C.随机测量一株水稻,其株高在120cm以上的概率比株高在70cm以下的概率大
D.随机测量一株水稻,其株高在(80,90)和在(100,110)(单位:cm)的概率一样大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】湖北七市州高三5月23日联考后,从全体考生中随机抽取44名,获取他们本次考试的数学成绩![]() 和物理成绩
和物理成绩![]() ,绘制成如图散点图:
,绘制成如图散点图:
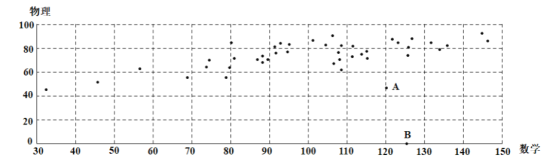
根据散点图可以看出![]() 与
与![]() 之间有线性相关关系,但图中有两个异常点
之间有线性相关关系,但图中有两个异常点![]() .经调查得知,
.经调查得知,![]() 考生由于重感冒导致物理考试发挥失常,
考生由于重感冒导致物理考试发挥失常,![]() 考生因故未能参加物理考试.为了使分析结果更科学准确,剔除这两组数据后,对剩下的数据作处理,得到一些统计的值:
考生因故未能参加物理考试.为了使分析结果更科学准确,剔除这两组数据后,对剩下的数据作处理,得到一些统计的值:![]()
![]()
![]() 其中
其中![]() ,
,![]() 分别表示这42名同学的数学成绩、物理成绩,
分别表示这42名同学的数学成绩、物理成绩,![]() ,2,…,42,
,2,…,42,![]() 与
与![]() 的相关系数
的相关系数![]() .
.
(1)若不剔除![]() 两名考生的数据,用44组数据作回归分析,设此时
两名考生的数据,用44组数据作回归分析,设此时![]() 与
与![]() 的相关系数为
的相关系数为![]() .试判断
.试判断![]() 与
与![]() 的大小关系,并说明理由;
的大小关系,并说明理由;
(2)求![]() 关于
关于![]() 的线性回归方程,并估计如果
的线性回归方程,并估计如果![]() 考生参加了这次物理考试(已知
考生参加了这次物理考试(已知![]() 考生的数学成绩为125分),物理成绩是多少?
考生的数学成绩为125分),物理成绩是多少?
(3)从概率统计规律看,本次考试七市州的物理成绩![]() 服从正态分布
服从正态分布![]() ,以剔除后的物理成绩作为样本,用样本平均数
,以剔除后的物理成绩作为样本,用样本平均数![]() 作为
作为![]() 的估计值,用样本方差
的估计值,用样本方差![]() 作为
作为![]() 的估计值.试求七市州共50000名考生中,物理成绩位于区间(62.8,85.2)的人数
的估计值.试求七市州共50000名考生中,物理成绩位于区间(62.8,85.2)的人数![]() 的数学期望.
的数学期望.
附:①回归方程![]() 中:
中: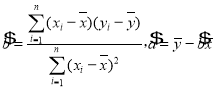
②若![]() ,则
,则![]()
③![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点
的焦点![]() 到准线
到准线![]() 的距离为2,直线
的距离为2,直线![]() 与抛物线交于不同的两点
与抛物线交于不同的两点![]() ,
,![]() .
.
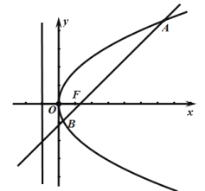
(1)求抛物线的方程;
(2)是否存在与![]() 的取值无关的定点
的取值无关的定点![]() ,使得直线
,使得直线![]() ,
,![]() 的斜率之和恒为定值?若存在,求出所有点
的斜率之和恒为定值?若存在,求出所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com