
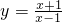 在区间[2,6]上的最大值为3;④函数
在区间[2,6]上的最大值为3;④函数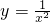 在定义域上是减函数.
在定义域上是减函数. ,在[2,6]上单调减,故x=2时,函数取得最大值
,在[2,6]上单调减,故x=2时,函数取得最大值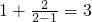 ;④函数
;④函数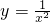 为偶函数,在(0,+∞)上单调减,在(-∞,0)上单调增,由此可得结论.
为偶函数,在(0,+∞)上单调减,在(-∞,0)上单调增,由此可得结论. ,在[2,6]上单调减,故x=2时,函数取得最大值
,在[2,6]上单调减,故x=2时,函数取得最大值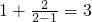 ,故③正确;
,故③正确;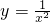 为偶函数,在(0,+∞)上单调减,在(-∞,0)上单调增,故④错误
为偶函数,在(0,+∞)上单调减,在(-∞,0)上单调增,故④错误

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
| x2+x+1 |
| 1 |
| 5x2-4x+11 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2013届安徽省宿州市度高二下学期第一次阶段理科数学试卷(解析版) 题型:填空题
已知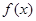 的导数为
的导数为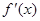 ,下列说法正确的有________.
,下列说法正确的有________.
①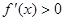 的解集为函数的增区间.
的解集为函数的增区间.
②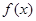 在区间上递增则
在区间上递增则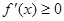 .
.
③极大值一定大于极小值.
④极大值有可能小于极小值.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
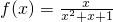 不存在承托函数;
不存在承托函数;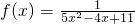 ,若函数g(x)的图象恰为f(x)在点
,若函数g(x)的图象恰为f(x)在点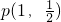 处的切线,则g(x)为函数f(x)的一个承托函数.
处的切线,则g(x)为函数f(x)的一个承托函数.查看答案和解析>>
科目:高中数学 来源:2008-2009学年北京101中学高三(上)数学试卷(理科)(解析版) 题型:填空题
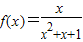 不存在承托函数;
不存在承托函数; ,若函数g(x)的图象恰为f(x)在点
,若函数g(x)的图象恰为f(x)在点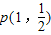 处的切线,则g(x)为函数f(x)的一个承托函数.
处的切线,则g(x)为函数f(x)的一个承托函数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com