
【题目】定义域为R的函数f(x)= ![]() (x)+bf(x)+c=0恰有5个不同的实数解x1 , x2 , x3 , x4 , x5 , 则f(x1+x2+x2+x4+x5)等于 ( )
(x)+bf(x)+c=0恰有5个不同的实数解x1 , x2 , x3 , x4 , x5 , 则f(x1+x2+x2+x4+x5)等于 ( )
A.0
B.21g2
C.31g2
D.1
【答案】C
【解析】解:当x=2时,f(x)=1,则由f2(x)+bf(x)+c=0得1+b+c=0.∴x1=2,c=﹣b﹣1.
当x>2时,f(x)=lg(x﹣2),由f2(x)+bf(x)+c=0得[lg(x﹣2)]2+blg(x﹣2)﹣b﹣1=0,解得lg(x﹣2)=1,x2=12或lg(x﹣2)=b,x3=2+10b .
当x<2时,f(x)=lg(2﹣x),由f2(x)+bf(x)+c=0得[lg(2﹣x)]2+blg(2﹣x)﹣b﹣1=0),解得lg(2﹣x)=1,x4=﹣8或lg(2﹣x)=b,x5=2﹣10b .
∴f(x1+x2+x3+x4+x5)=f(2+12+2+10b﹣8+2﹣10b)=f(10)=lg|10﹣2|=lg8=3lg2.
故选C.


科目:高中数学 来源: 题型:
【题目】【选修4-4:坐标系与参数方程】
在极坐标系中,已知点![]() 到直线
到直线![]() 的距离为3.
的距离为3.
(1)求实数![]() 的值;
的值;
(2)设![]() 是直线
是直线![]() 上的动点,
上的动点, ![]() 在线段
在线段![]() 上,且满足
上,且满足![]() ,求点
,求点![]() 的轨迹方程,并指出轨迹是什么图形.
的轨迹方程,并指出轨迹是什么图形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,我国PM2.5标准采用世卫组织设定的最宽限值,即PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某市环保局从市区2017年上半年每天的PM2.5监测数据中随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶)
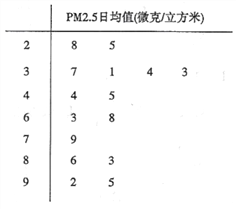
(1)从这15天的数据中任取一天,求这天空气质量达到一级的概率;
(2)从这15天的数据中任取3天的数据,记![]() 表示其中空气质量达到一级的天数,求
表示其中空气质量达到一级的天数,求![]() 的分布列;
的分布列;
(3)以这15天的PM2.5的日均值来估计一年的空气质量情况,(一年按360天来计算),则一年中大约有多少天的空气质量达到一级.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中是假命题的是( )
A.?![]() ∈R,使sin(
∈R,使sin(![]() )=
)=![]() +sinβ
+sinβ
B.?![]() ∈R,函数f(x)=sin(
∈R,函数f(x)=sin(![]() )都不是偶函数
)都不是偶函数
C.?m∈R,使f(x)=(m-1)·m2-4m+3是幂函数,且在(0,+∞)上单调递减
D.?![]() >0,函数f(x)=ln2x+lnx-
>0,函数f(x)=ln2x+lnx-![]() 有零点
有零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若f(x)为二次函数,﹣1和3是方程f(x)﹣x﹣4=0的两根,f(0)=1
(1)求f(x)的解析式;
(2)若在区间[﹣1,1]上,不等式f(x)>2x+m有解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】心理学家通过研究学生的学习行为发现;学生的接受能力与老师引入概念和描述问题所用的时间相关,教学开始时,学生的兴趣激增,学生的兴趣保持一段较理想的状态,随后学生的注意力开始分散,分析结果和实验表明,用f(x)表示学生掌握和接受概念的能力,x表示讲授概念的时间(单位:min),可有以下的关系:f(x)= 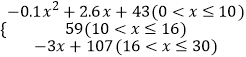
(Ⅰ)开讲后第5min与开讲后第20min比较,学生的接受能力何时更强一些?
(Ⅱ)开讲后多少min学生的接受能力最强?能维持多少时间?
(Ⅲ)若一个新数学概念需要55以上(包括55)的接受能力以及13min时间,那么老师能否在学生一直达到所需接受能力的状态下讲授完这个概念?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
, ![]() )为奇函数,且相邻两对称轴间的距离为
)为奇函数,且相邻两对称轴间的距离为![]() .
.
(1)当![]() 时,求
时,求![]() 的单调递减区间;
的单调递减区间;
(2)将函数![]() 的图象沿
的图象沿![]() 轴方向向右平移
轴方向向右平移![]() 个单位长度,再把横坐标缩短到原来的
个单位长度,再把横坐标缩短到原来的![]() (纵坐标不变),得到函数
(纵坐标不变),得到函数![]() 的图象.当
的图象.当![]() 时,求函数
时,求函数![]() 的值域.
的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com