练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知抛物线上横坐标为的点到焦点的距离为.

    （1）求抛物线的方程；

    （2）若过点的直线与抛物线交于不同的两点，且以为直径的圆过坐标原点，求的面积。

    【答案】（1）；（2）

    【解析】试题分析：（1）由抛物线上横坐标为的点到焦点的距离为可得 解得，从而可得抛物线的方程；（2）先讨论直线斜率不存在时的情况，当斜率存在时，设直线方程为联立，消去得 ，根据韦达定理、平面向量数量积公式以及弦长公式、点到直线距离公式与三角形面积公式可求得的面积.

    试题解析：（1）依题意： 解得，所以抛物线的方程为

    （2）依题意：若直线斜率不存在时，直线与抛物线只有一个交点，不符合题意；

    所以设直线方程为

    联立，消去得

    所以

    又

    因为以为直径的圆过坐标原点，所以，

    所以

    解得，由，点到直线的距离为

    所以。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】解下列关于x的不等式：

    （1）； （2）x2-ax-2a2≤0（a∈R）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设公差不为零的等差数列{an}的前5项的和为55，且a2 ， ﹣9成等比数列．
    （1）求数列{an}的通项公式．
    （2）设数列bn= ，求证：数列{bn}的前n项和Sn＜ ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下图是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:

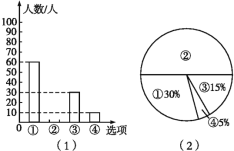
    (1)本次一共调查了多少名学生.(2)在图(1)中将②对应的部分补充完整.

    (3)若该校有3 000名学生,你估计全校有多少名学生平均每天参加体育活动的时间在0.5时以下?

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在某城市气象部门的数据中，随机抽取100天的空气质量指数的监测数据如表：

    空气质量指数t

    （0，50]

    （50，100]

    （100，150]

    （150，200）

    （200，300]

    （300，+∞）

    质量等级

    优

    良

    轻微污染

    轻度污染

    中度污染

    严重污染

    天数K

    5

    23

    22

    25

    15

    10

    （1）若该城市各医院每天收治上呼吸道病症总人数y与当天的空气质量（取整数）存在如下关系 且当t＞300时，y＞500，估计在某一医院收治此类病症人数超过200人的概率；

    （2）若在（1）中，当t＞300时，y与t的关系拟合的曲线为，现已取出了10对样本数据（ti，yi）（i=1，2，3，…，10），且知 试用可线性化的回归方法，求拟合曲线的表达式．（附：线性回归方程中， ， ．）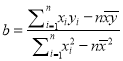

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某商品一年内出厂价格在6元的基础上按月份随正弦曲线波动，已知3月份达到最高价格8元，7月份价格最低为4元，该商品在商店内的销售价格在8元基础上按月份随正弦曲线波动，5月份销售价格最高为10元，9月份销售价最低为6元，假设商店每月购进这种商品m件，且当月销完，你估计哪个月份盈利最大?

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，，函数，若的图象上相邻两条对称轴的距离为，图象过点.

    （1）求表达式和的单调增区间；

    （2）将函数的图象向右平移个单位，再将图象上各点的横坐标伸长到原来的2倍（纵坐标不变），得到函数的图象，若函数在区间上有且只有一个零点，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义在R上的函数，其中a为常数.

    （I）若x=1是函数的一个极值点，求a的值

    （II）若函数在区间（－1，0）上是增函数，求a的取值范围

    （III）若函数，在x=0处取得最大值，求正数a的取值范围

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分分）

    已知半径为的圆的圆心在轴上，圆心的横坐标是整数，且与直线相切．

    （Ⅰ）求圆的方程．

    （Ⅱ）设直线与圆相交于， 两点，求实数的取值范围．

    （Ⅲ）在（Ⅱ）的条件下，是否存在实数，使得点到， 两点的距离相等，若存在，求出实数的值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案