
分析 (1)解法1:设⊙M的方程为一般式,根据条件列出方程组,求解后即可求出⊙M的方程;
解法2:根据A(1,0),B(1,4)的横坐标相同设M(m,2),由半径相等和两点之间的距离公式列出方程求出m,可得⊙M的方程;
解法3:由向量的坐标运算求出$\overrightarrow{CA},\overrightarrow{CB}$,由向量的数量积运算求出$\overrightarrow{CA}•\overrightarrow{CB}$和模,判断出△ACB是等腰直角三角形,由直角三角形外接圆的性质求出⊙M的方程;
(2)对直线l的斜率存在问题分类讨论,根据点到直线的距离公式和弦长公式列出方程,求出直线的斜率,即可得到直线方程.
解答 解:(1)解法1:设⊙M的方程为:x2+y2+Dx+Ey+F=0,…(2分)
则由题意得$\left\{\begin{array}{l}1+D+F=0\\ 17+D+4E+F=0\\ 13+3D+2E+F=0\end{array}\right.$,解得$\left\{\begin{array}{l}D=-2\\ E=-4\\ F=1\end{array}\right.$,…(6分),
∴⊙M的方程为x2+y2-2x-4y+1=0,或(x-1)2+(y-2)2=4…(8分)
解法2:∵A(1,0),B(1,4)的横坐标相同,故可设M(m,2),…(3分)
由MA2=MC2得(m-1)2+4=(m-3)2,解得m=1…(6分)
∴⊙M的方程为(x-1)2+(y-2)2=4,或x2+y2-2x-4y+1=0…(8分)
解法3:∵A(1,0),B(1,4),C(3,2),∴$\overrightarrow{CA}=(2,2),\overrightarrow{CB}=(2,-2)$,
∴$\overrightarrow{CA}•\overrightarrow{CB}=0,|{\overrightarrow{CA}}|=|{\overrightarrow{CB}}|$,则△ACB是等腰直角三角形,
因而△ACB圆心为(1,2),半径为2,…(6分)
∴⊙M的方程为(x-1)2+(y-2)2=4…(8分)
(2)当直线l与x轴垂直时,l方程为x=0,它截⊙M得弦长恰为$2\sqrt{3}$…(9分)
当直线l的斜率存在时,设l:y=kx+4…(10分)
∵圆心到直线y=kx+4的距离d=$\frac{{|{k+2}|}}{{\sqrt{{k^2}+1}}}$…(11分)
由勾股定理得${(\frac{{|{k+2}|}}{{\sqrt{{k^2}+1}}})^2}+{(\frac{{2\sqrt{3}}}{2})^2}=4$,解得$k=-\frac{3}{4}$…(14分)
故直线l的方程为x=0或3x+4y-16=0…(15分)
点评 本题考查圆的方程求法:待定系数法和几何法,直线与圆相交的弦长问题常根据半弦长,弦心距,半径构成直角三角形,利用勾股定理求解,考查一题多解,以及化简、计算能力.


科目:高中数学 来源: 题型:填空题
 已知三棱锥的三视图的正视图是等腰三角形,俯视图是边长为$\sqrt{3}$的等边三角形,侧视图是直角三角形,且三棱锥的外接球表面积为8π,则三棱锥的高为2.
已知三棱锥的三视图的正视图是等腰三角形,俯视图是边长为$\sqrt{3}$的等边三角形,侧视图是直角三角形,且三棱锥的外接球表面积为8π,则三棱锥的高为2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 20072 | D. | 2007 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
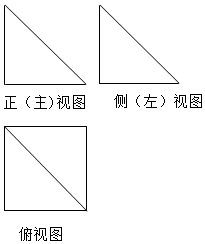 已知一个几何体的三视图如图所示,其中正视图和俯视图是全等的等腰直角三角形,则这个几何体外接球体积与该几何体的体积之比为( )
已知一个几何体的三视图如图所示,其中正视图和俯视图是全等的等腰直角三角形,则这个几何体外接球体积与该几何体的体积之比为( )| A. | $\frac{3\sqrt{3}}{2}$π | B. | $\frac{\sqrt{3}}{4}$π | C. | $\frac{3\sqrt{3}}{4}$π | D. | $\frac{\sqrt{3}}{8}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
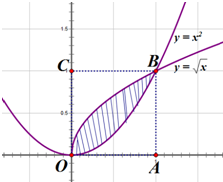 如图,设区域D={(x,y)|0≤x≤1,0≤y≤1,向区域内随机投一点,且投入到区域内任一点都是等可能的,则点落到由曲线y=$\sqrt{x}$与y=x2所围成阴影区域内的概率是( )
如图,设区域D={(x,y)|0≤x≤1,0≤y≤1,向区域内随机投一点,且投入到区域内任一点都是等可能的,则点落到由曲线y=$\sqrt{x}$与y=x2所围成阴影区域内的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com