
分析 若命题p为真命题:则3-m>m-1>0,解得m范围.若命题q为真命题:则△<0,解得m取值范围.再利用复合命题的真假判定方法即可得出.
解答 解:∵命题p:“方程$\frac{{x}^{2}}{m-1}$+$\frac{{y}^{2}}{3-m}$=1表示的曲线是焦点在y轴上的椭圆”,
∴3-m>m-1>0,解得1<m<2.
命题q:“函数f(x)=lg(x2-mx+$\frac{9}{16}$)的定义域为R”,∴△=m2-4×$\frac{9}{16}$<0,解得$-\frac{3}{2}$$<m<\frac{3}{2}$.
(1)由命题p为真命题,则实数m的取值范围是(1,2);
(2)若p∧q是真命题,则p与q都为真命题,∴$\left\{\begin{array}{l}{1<m<2}\\{-\frac{3}{2}<m<\frac{3}{2}}\end{array}\right.$,解得$1<m<\frac{3}{2}$.
∴实数m的取值范围是$(1,\frac{3}{2})$.
点评 本题考查了椭圆的标准方程及其性质、对数函数的性质、复合命题的真假的判定方法,考查了推理能力与计算能力,属于中档题.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
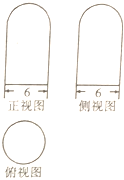 某建筑物是由一个半球和一个圆柱组成,半球的体积是圆柱体积的$\frac{1}{4}$,其三视图如图所示,现需要在该建筑物表面涂一层防晒涂料,若每π个平方单位所需涂料费用为100元,则共需涂料费用( )
某建筑物是由一个半球和一个圆柱组成,半球的体积是圆柱体积的$\frac{1}{4}$,其三视图如图所示,现需要在该建筑物表面涂一层防晒涂料,若每π个平方单位所需涂料费用为100元,则共需涂料费用( )| A. | 6600元 | B. | 7500元 | C. | 8400元 | D. | 9000元 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 从某小学随机抽取100名学生,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图),若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[120,130)内的学生中选取的人数应为( )
从某小学随机抽取100名学生,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图),若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[120,130)内的学生中选取的人数应为( )| A. | 10 | B. | 9 | C. | 8 | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com