
 从某小学随机抽取100名学生,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图),若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[120,130)内的学生中选取的人数应为( )
从某小学随机抽取100名学生,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图),若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[120,130)内的学生中选取的人数应为( )| A. | 10 | B. | 9 | C. | 8 | D. | 7 |
分析 由频率分布直方图先求出a=0.03,再求出身高在[120,130),[130,140),[140,150]三组内的学生人数,由此利用分层抽样方法能求出从身高在[120,130)内的学生中选取的人数.
解答 解:由频率分布直方图得:
10a=1-(0.005+0.035+0.020+0.010)×10=0.3,
解得a=0.03.
∴身高在[120,130),[130,140),[140,150]三组内的学生人数分别为:
0.03×10×100=30,0.02×10×100=20,0.01×10×100=10,
∴从身高在[120,130),[130,140),[140,150]三组内的学生中,
用分层抽样的方法选取18人参加一项活动,
则从身高在[120,130)内的学生中选取的人数应为:30×$\frac{18}{30+20+10}$=9(人).
故选:B.
点评 本题考查分层抽样的应用,是基础题,解题时要认真审题,注意分层抽样的性质的合理运用.


科目:高中数学 来源: 题型:选择题
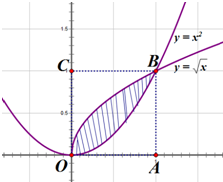 如图,设区域D={(x,y)|0≤x≤1,0≤y≤1,向区域内随机投一点,且投入到区域内任一点都是等可能的,则点落到由曲线y=$\sqrt{x}$与y=x2所围成阴影区域内的概率是( )
如图,设区域D={(x,y)|0≤x≤1,0≤y≤1,向区域内随机投一点,且投入到区域内任一点都是等可能的,则点落到由曲线y=$\sqrt{x}$与y=x2所围成阴影区域内的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 气温x (℃) | 18 | 13 | 10 | -1 |
| 山高y(km) | 24 | 34 | 38 | 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{21}{44}$ | B. | $\frac{15}{22}$ | C. | $\frac{21}{50}$ | D. | $\frac{9}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知某几何体的正(主)视图,侧(左)视图和俯视图均为边长为1的正方形(如图),若该几何体的顶点都在同一球面上,则此球的表面积为( )
已知某几何体的正(主)视图,侧(左)视图和俯视图均为边长为1的正方形(如图),若该几何体的顶点都在同一球面上,则此球的表面积为( )| A. | 4π | B. | 3π | C. | 2π | D. | π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com