
分析 利用同角三角函数的基本关系求得cosα和cosβ的值,再利用两角差的余弦公式求得cos(α+β)的值,可得α+β 的值.
解答 解:∵sinα=$\frac{{\sqrt{5}}}{5}$,sinβ=$\frac{{\sqrt{10}}}{10}$,且α,β均为锐角,
∴cosα=$\sqrt{{1-sin}^{2}α}$=$\frac{2\sqrt{5}}{5}$,cosβ=$\sqrt{{1-sin}^{2}β}$=$\frac{3\sqrt{10}}{10}$,
则cos(α+β)=cosαcosβ-sinαsinβ=$\frac{2\sqrt{5}}{5}•\frac{3\sqrt{10}}{10}$-$\frac{\sqrt{5}}{5}•\frac{\sqrt{10}}{10}$=$\frac{\sqrt{2}}{2}$.
再根据α+β∈(0,π),求得α+β=$\frac{π}{4}$,
故答案为:$\frac{π}{4}$.
点评 本题主要考查同角三角函数的基本关系,两角差的余弦公式的应用,属于基础题.


 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 类比推理 | B. | 演绎推理 | C. | 归纳推理 | D. | 传递性推理 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | -2 | -1 | 0 | 1 | 2 |
| y | 5 | 4 | 2 | 2 | 1 |
| A. | $\stackrel{∧}{y}$=-x+2.8 | B. | $\stackrel{∧}{y}$=-x+3 | C. | $\stackrel{∧}{y}$=-1.2x+2.6 | D. | $\stackrel{∧}{y}$=2x+2.7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
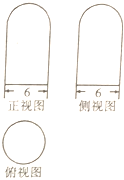 某建筑物是由一个半球和一个圆柱组成,半球的体积是圆柱体积的$\frac{1}{4}$,其三视图如图所示,现需要在该建筑物表面涂一层防晒涂料,若每π个平方单位所需涂料费用为100元,则共需涂料费用( )
某建筑物是由一个半球和一个圆柱组成,半球的体积是圆柱体积的$\frac{1}{4}$,其三视图如图所示,现需要在该建筑物表面涂一层防晒涂料,若每π个平方单位所需涂料费用为100元,则共需涂料费用( )| A. | 6600元 | B. | 7500元 | C. | 8400元 | D. | 9000元 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com