
 (t是参数,0≤α<π),以坐标原点为极点,x轴的非负半轴为极轴,建立极坐标系,曲线C的极坐标方程为ρ=4cos(θ-
(t是参数,0≤α<π),以坐标原点为极点,x轴的非负半轴为极轴,建立极坐标系,曲线C的极坐标方程为ρ=4cos(θ- ),直线l与曲线C相交于A、B两点.
),直线l与曲线C相交于A、B两点. ,求α的取值范围.
,求α的取值范围. ),可化为
),可化为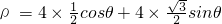 ,
,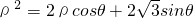 ,
,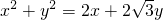 ,
,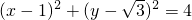 ,
, ,半径r=2的圆.
,半径r=2的圆. ,
,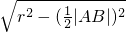 ,
,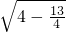 =
= .
. 时,圆心C到直线l的距离是1
时,圆心C到直线l的距离是1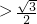 ,不成立;
,不成立;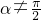 时,设k=tanα,则l:
时,设k=tanα,则l: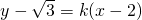 .
.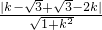 =
=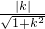
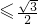 ,
,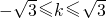 ,即
,即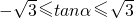 .
.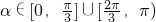 ,即为α的取值范围.
,即为α的取值范围. 代入曲线C的方程
代入曲线C的方程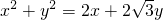 ,
,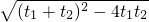 =
=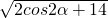 ,
,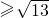 ,
,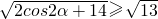 ,
,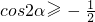 ,
,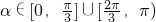 ,即为α的取值α
,即为α的取值α 三者之间的关系:d=
三者之间的关系:d=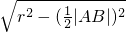 ,及|AB|
,及|AB|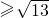 ,即可求出答案;
,即可求出答案;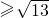 即可得出的答案.
即可得出的答案. 三者之间的关系:d=
三者之间的关系:d=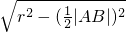 ,及直线l的参数方程中的t的意义是解题的关键.
,及直线l的参数方程中的t的意义是解题的关键. 

 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:高中数学 来源: 题型:
| π | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| 3π |
| 2 |
| AC |
| BC |
| π |
| 2 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com