
| ? |
| y |
| 5 |
| 22 |
| 1 |
| 2 |
| 50+60 |
| 2 |
| 20+30+40+50+60+70 |
| 6 |
| 1 |
| 4.4 |
| 5 |
| 22 |
| AB |
| AC |
| AB |
| AC |
| 5 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |


 ø⁄À„–°◊¥‘™ø⁄À„ÀŸÀ„ÃÏÃÏ¡∑œµ¡–¥∞∏
ø⁄À„–°◊¥‘™ø⁄À„ÀŸÀ„ÃÏÃÏ¡∑œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
| x2-x-2 |
| 1 |
| 3 |
| 1 |
| 3 |
| ¶– |
| 8 |
| ¶– |
| 4 |
| 1 |
| 2 |
| 2 |
| 2 |
| A°¢.1∏ˆ | B°¢2∏ˆ |
| C°¢3∏ˆ | D°¢.4∏ˆ |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
| 1 |
| 3 |
| 1 |
| 3 |
| ¶– |
| 8 |
| ¶– |
| 4 |
| AB |
| DC |
| BC |
| DA |
| a |
| b |
| a |
| b |
| a |
| b |
| A°¢1 | B°¢2 | C°¢3 | D°¢4 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
| 1 |
| 2 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
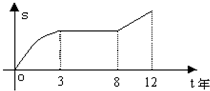 ƒ≥π§≥ß12ƒÍ¿¥ƒ≥≤˙∆∑◊Ð≤˙¡øS”Î ±º‰t£®ƒÍ£©µƒ∫Ø ˝πÿœµ»ÁÕºÀ˘ 棨œ¬¡–Àƒ÷÷Àµ∑®£∫
ƒ≥π§≥ß12ƒÍ¿¥ƒ≥≤˙∆∑◊Ð≤˙¡øS”Î ±º‰t£®ƒÍ£©µƒ∫Ø ˝πÿœµ»ÁÕºÀ˘ 棨œ¬¡–Àƒ÷÷Àµ∑®£∫≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com