
| A. | [10,+∞) | B. | [7,+∞) | C. | [-3,+∞) | D. | [0,+∞) |
分析 求出f(x)min=-8,g(x)min=-1-m,根据任意的x1∈[-4,-2),均存在${x_2}∈[{{e^{-1}},{e^2}}]$使得不等式f(x1)-g(x2)≥0恒成立,得出f(x)min≥g(x)min,即可求出实数m的取值范围.
解答 解:由题意,f(x+4)=$\frac{1}{2}$f(x+2)=$\frac{1}{4}$f(x),
设x∈[-4,-2),则x+4∈[0,2),∴f(x)=4f(x+4)=$\left\{\begin{array}{l}{2-8{(x+4)}^{2},-4≤x<-3}\\{-{2}^{3-|-x-\frac{5}{2}|},-3≤x<-2}\end{array}\right.$.
-4≤x<-3时,f(x)∈(-6,2];-3≤x<-2时,f(x)∈[-8,-4$\sqrt{2}$]
∴f(x)min=-8,
∵g(x)=lnx-m,${x_2}∈[{{e^{-1}},{e^2}}]$,
∴g(x)min=-1-m,
∵任意的x1∈[-4,-2),均存在${x_2}∈[{{e^{-1}},{e^2}}]$使得不等式f(x1)-g(x2)≥0恒成立,
∴f(x)min≥g(x)min,
∴-8≥-1-m,
∴m≥7.
故选:B.
点评 本题考查恒成立问题,考查函数的最值,正确转化为f(x)min≥g(x)min是关键.


科目:高中数学 来源: 题型:解答题
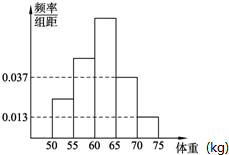 某省组织部为了了解今年全省高三毕业班准备报考飞行员的学生的体重情况,对该省某校高三毕业班准备报考飞行员的学生的体重进行了统计,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
某省组织部为了了解今年全省高三毕业班准备报考飞行员的学生的体重情况,对该省某校高三毕业班准备报考飞行员的学生的体重进行了统计,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $C_n^{m-1}$ | B. | $A_n^{m-1}$ | C. | $C_n^m$ | D. | $A_n^m$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x<2 } | B. | {x|0<x<2} | C. | {x|0≤x<l} | D. | {x|0<x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
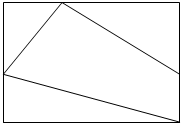 用5种不同的颜色给图中四个区域涂色,允许同一种颜色使用多次,但相邻区域必须涂不同颜色,不同的涂色方法有( )
用5种不同的颜色给图中四个区域涂色,允许同一种颜色使用多次,但相邻区域必须涂不同颜色,不同的涂色方法有( )| A. | 180 | B. | 240 | C. | 160 | D. | 320 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com