练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

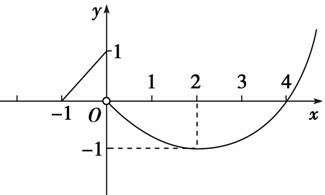
    对如图，定义在[－1，＋∞)上的函数f(x)的图象由一条线段及抛物线的一部分组成，求f(x)的解析式．


    解析：当－1≤x≤0时，设解析式为y＝kx＋b，

    由图象有得所以y＝x＋1.

    当x＞0时，设解析式为y＝a(x－2)2－1，

    因为图象过点(4,0)，所以0＝a(4－2)2－1，解得a＝.

    所以y＝(x－2)2－1.

    综上，函数f(x)在[－1，＋∞)上的解析式为

    f(x)＝


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    过三点确定一个平面

    ②梯形可以确定一个平面

    ③两两相交的三条直线最多可以确定三个平面

    ④如果两个平面有三个公共点，则这两个平面重合．

    A．1       B．2       C．3       D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数y＝(1－x2)的值域是(　　)

    A．[0，＋∞)           B．(0,1]

    C．(0,1)               D．[0,1]

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝－(a＞0, x＞0)，

    (1)求证：f(x)在(0，＋∞)上是单调递增函数；

    (2)若f(x)在上的值域是，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    将函数y＝2x＋1的图象按向量a平移得到函数y＝2x＋1的图象，则(　　)

    A．a＝(－1，－1)

    B．a＝(1，－1)

    C．a＝(1,1)

    D．a＝(－1,1)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a，b∈R，则“log2a＞log2b”是 “a＜b”的(　　)

    A．充分不必要条件          B．必要不充分条件

    C．充要条件                D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    定义域为R的四个函数y＝x3，y＝2x，y＝x2＋1，y＝2 sin x中，奇函数的个数是(　　)

    A．4          B．3          C．2         D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若曲线f(x)＝、g(x)＝xa在点P(1,1)处的切线分别为l1、l2，且l1⊥l2，则a的值为(　　)

    A．－2         B．2       C.         D．－

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)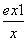＝，x≠0.

    (1)判断函数f(x)在(0，＋∞)上的单调性；

    (2)证明：对任意正数a，存在正数x，使不等式|f(x)－1|＜a成立．

    查看答案和解析>>

    同步练习册答案