
设函数f(x)=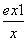 ,x≠0.
,x≠0.
(1)判断函数f(x)在(0,+∞)上的单调性;
(2)证明:对任意正数a,存在正数x,使不等式|f(x)-1|<a成立.
解析:(1)f′(x)=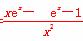 =
=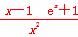 ,
,
令h(x)=(x-1)ex+1,则h ′(x)=ex+ex(x-1)=xex,
′(x)=ex+ex(x-1)=xex,
当x>0时,h′(x)=xex>0,∴h(x)是(0,+∞)上的增函数,
所以h(x)>h(0)=0,
故f′(x)=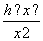 >0,即函数f(x)是(0,+∞)上的增函数.
>0,即函数f(x)是(0,+∞)上的增函数.
(2)|f(x)-1|=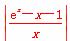 ,
,
当x>0时,令g(x)=ex-x-1,则g′(x)=ex-1>0,
故g(x)>g(0)=0,所以|f(x)-1|=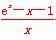 ,
,
原不等式化为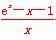 <a,即ex-(1+a)x-1<0,
<a,即ex-(1+a)x-1<0,
令φ(x)=ex-(1+a)x-1,则φ′(
 x)=ex-(1+a),
x)=ex-(1+a),
由φ′(x)=0得: ex=1+a,解得x=ln(1+a),
ex=1+a,解得x=ln(1+a),
当0<x<ln(1+a)时,φ′(x)<0;
当x>ln(1+a)时,φ′(x)>0.
故当x=ln(1+a)时,φ(x)取得最小值φ(ln(1+a))=a-(1+a)ln(1+a),
令s(a)= -ln(1+a),a>0则s′(a)=
-ln(1+a),a>0则s′(a)=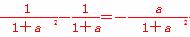 <0.故s(a)<s(0)=0,即φ(ln(1+a))=a-(1+a)ln(1+a)<0.
<0.故s(a)<s(0)=0,即φ(ln(1+a))=a-(1+a)ln(1+a)<0.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
设 f(x),g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)>0,且g(-3)=0,则不等式f(x)g(x)<0的解集是________________.
f(x),g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)>0,且g(-3)=0,则不等式f(x)g(x)<0的解集是________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
有一个长度为5 m的梯子贴靠在笔直的墙上,假设其下端沿地板以3 m/s的速度离开墙脚滑动,当其下端离开墙脚1.4 m 时,梯子上端下滑的速度为____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
某工厂采用高科技改革,在2年内产值的月增长率都是a,则这2年内第2年某月的产值比第1年相应月产值的增长率为( )
A.a12- 1 B.(1+a)12-1
1 B.(1+a)12-1
C.a D.a-1
查看答案和解析>>
科目:高中数学 来源: 题型:
已知a,b,c∈R,函数f(x)=ax2+bx+c.若f(0)=f(4)>f(1),则( )
A.a>0,4a+b=0  B.a<0,4a+b=0
B.a<0,4a+b=0
C.a>0,2a+b=0 D.a<0,2a+b=0
查看答案和解析>>
科目:高中数学 来源: 题型:
有这样的算法:
第一步,设i的值为1.
第二步,设sum的值为0.
第三步,若i≤100,执行第四步,否则转去执行第七步.
第四步,计算sum+(i+1)/i,并将 结果代替sum.
结果代替sum.
第五步,计算i+1,并将结果代替i.
第六步,转去执行第三步.
第七步,输出sum的值,并结束算法.
这个算法是 ( )
A.求2+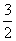 +
+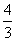 +…+
+…+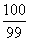 的和
的和
B.求2+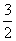 +
+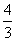 +…+
+…+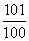 的和
的和
C.求1+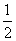 +
+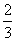 +…+
+…+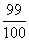 的和
的和
D.求 1+
1+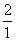 +
+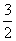
 +
+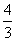 +…+
+…+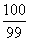 的和
的和
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com