
| A. | 0 | B. | 2019 | C. | -2019 | D. | 2018×2019 |
分析 通过分析可知a2k-1+a2k=2(k为正整数),进而并项相加即得结论.
解答 解:由题可知an=$\left\{\begin{array}{l}{{n}^{2}-(n+1)^{2}=-2n-1,}&{n为正奇数}\\{-{n}^{2}+(n+1)^{2}=2n+1,}&{n为正偶数}\end{array}\right.$,
所以a2k-1+a2k=2(k为正整数),
所以a1+a2+a3+…+a2017
=(-2-1)+(4+1)+(-6-1)+(8+1)+…+(-4030-1)+(4032+1)+(-4034-1)
=2016-4034-1
=-2019,
故选:C.
点评 本题考查数列的求和,考查并项相加法,考查分类讨论的思想,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,n⊥β,m⊥n,则α⊥β | B. | 若m?α,n?α,n⊥l,则l⊥α | ||
| C. | 若m∥α,n⊥β,α⊥β,则m∥n | D. | 若l⊥α,l⊥β,则α∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 一次购物量 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件及以上 |
| 顾客数(人) | x | 30 | 25 | y | 10 |
| 结算时间(分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
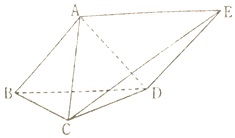 如图,在多面体ABCDE中,ABDE是平行四边形,AB、AC、AD两两垂直.
如图,在多面体ABCDE中,ABDE是平行四边形,AB、AC、AD两两垂直.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
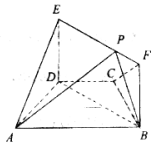 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com