设函数f(x)=x2ex-1+ax3+bx2(其中e是自然对数的底数),已知x=-2和x=1为函数f(x)的极值点.
(Ⅰ)求实数a和b的值;
(Ⅱ)讨论函数f(x)的单调性;
(Ⅲ)是否存在实数M,使方程f(x)=M有4个不同的实数根?若存在,求出实数M的取值范围;若不存在,请说明理由.
解:(Ⅰ)求导函数,可得f′(x)=(x
2+2x)e
x-1+3ax
2+2bx,…(1分)
∵x=-2和x=1为函数f(x)的极值点,
∴f′(-2)=f′(1)=0,…(2分)
即
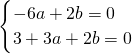
,解得

,…(3分)
所以,
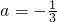
,b=-1.…(4分)
(Ⅱ)∵
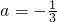
,b=-1,∴f′(x)=(x
2+2x)e
x-1-x
2-2x=(x
2+2x)(e
x-1-1),…(5分)
令f′(x)=0,解得x
1=-2,x
2=0,x
3=1,…(6分)
∵令f′(x)<0,可得x∈(-∞,-2)∪(0,1),令f′(x)>0,可得x∈(-2,0)∪(1,+∞),…(8分)
∴f(x)在区间(-2,0)和(1,+∞)上是单调递增的,在区间(-∞,-2)和(0,1)上是单调递减的.…(9分)
(Ⅲ)由(Ⅰ)得
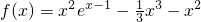
,由(Ⅱ)得函数的极大值为f(x)
极大值=f(0)=0,…(10分)
函数的极小值为f(x)
极小值=f(-2)=
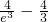
,和f(x)
极小值=f(1)=-

…(11分)
又
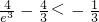
,…(12分)
f(-3)=(-3)
2e
-4+9-9=9e
-4>0,f(3)=3
2e
2-9-9=9(e
2-2)>0,…(13分)
通过上面的分析可知,当M∈
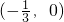
时方程f(x)=M恰有4个不等的实数根.
所以存在实数M,使方程f(x)=M有4个根,其M取值范围为
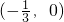
.…(14分)
分析:(Ⅰ)求导函数,利用x=-2和x=1为函数f(x)的极值点,可得导数值为0,即可方程,即可求实数a和b的值;
(Ⅱ)由导数的正负,即可确定函数的单调性;
(Ⅲ)确定函数的极大值与极小值,即可知使方程f(x)=M有4个根的M取值范围.
点评:本题考查导数知识的运用,考查函数的极值,考查函数的单调性,考查方程根问题,解题的关键是正确求导,确定函数的单调性与极值,属于中档题.

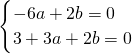 ,解得
,解得 ,…(3分)
,…(3分)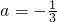 ,b=-1.…(4分)
,b=-1.…(4分)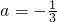 ,b=-1,∴f′(x)=(x2+2x)ex-1-x2-2x=(x2+2x)(ex-1-1),…(5分)
,b=-1,∴f′(x)=(x2+2x)ex-1-x2-2x=(x2+2x)(ex-1-1),…(5分)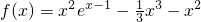 ,由(Ⅱ)得函数的极大值为f(x)极大值=f(0)=0,…(10分)
,由(Ⅱ)得函数的极大值为f(x)极大值=f(0)=0,…(10分)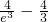 ,和f(x)极小值=f(1)=-
,和f(x)极小值=f(1)=- …(11分)
…(11分)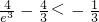 ,…(12分)
,…(12分)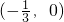 时方程f(x)=M恰有4个不等的实数根.
时方程f(x)=M恰有4个不等的实数根.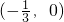 .…(14分)
.…(14分)

 一本好题口算题卡系列答案
一本好题口算题卡系列答案